프로그래밍
구글시트
데이터
수집, 시각화, 설명
모델링
확률모델, 새 확률변수, 통계모델, 연구계획
데이터분석
모수추정, 모수비교
표본종류: 대응표본
확률변수가정: 선형성, 정규성
새확률변수: 상관계수(공분산/표준편차곱)
표집분포: 상관계수 중심극한정리
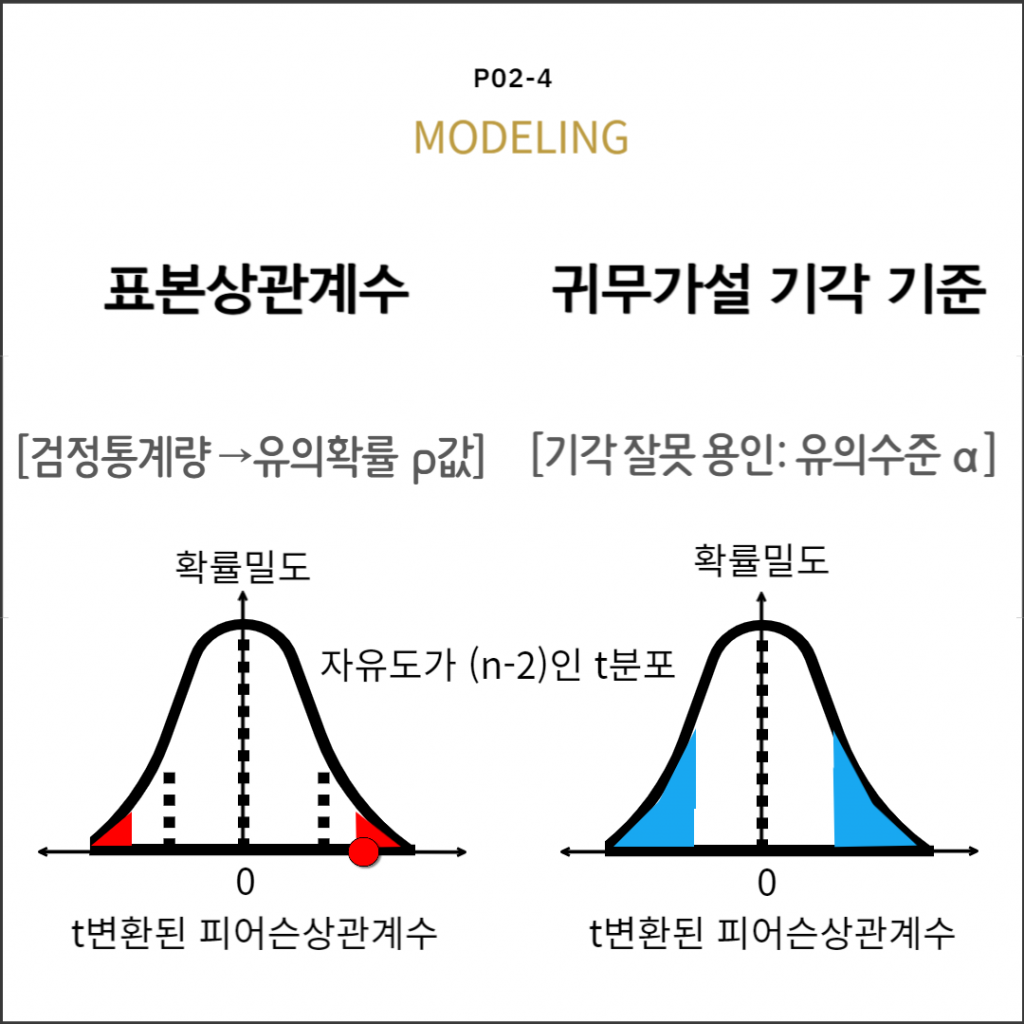
검정확률분포: t분포
검정통계량: 표본상관계수와 표준오차의 비
귀무가설: 마블링스코어와 등심지방함량의 상관계수는 0
가설검정: 유의확률과 유의수준을 비교
정규분포
$$f(y \, ; \mu_Y, \sigma_Y^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right)$$
여기서, $y$는 정규분포를 나타내는 확률변수, $Y$의 값(변량)
$\mu_Y$는 확률변수, $Y$의 기대값: 집단의 모평균
$\sigma_Y^2$는 확률변수, $Y$의 모분산: 집단의 모분산
확률변수 t
$$t = \dfrac{Z}{\sqrt{\dfrac{V} {\nu}}}$$
여기서, $Z$는 표준정규분포를 나타내는 확률변수
$V$는 자유도 $\nu$의 $\chi^2$분포를 나타내는 확률변수
$\nu$는 $V$의 자유도
t분포
$$f(t \, ; \nu)=\dfrac{\Gamma \left({\frac{\nu +1}{2}}\right)}{\sqrt{\nu \pi}\Gamma \left(\dfrac{\nu }{2}\right)}\left(1+\dfrac {t^2}{\nu }\right)^{-\frac{\nu +1}{2}}$$
여기서, $t$는 t분포를 나타내는 확률변수
$\nu$는 자유도
$\Gamma(\,\,)$는 감마함수
F = 집단간분산 / 집단내분산
$$F=\dfrac{MS_{B}}{MS_{W}}=\dfrac{\dfrac{SS_{B}}{k-1}}{\dfrac{SS_{W}}{n-k}}$$
여기서, $MS_B$는 집단간분산
$MS_W$는 집단내분산
$SS_B$는 집단간변동
$SS_W$는 집단내변동
$k$는 집단수
$n$은 표본크기
F = 회귀분산 / 잔차분산
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{SS_{Reg}}{k-1}}{\dfrac{SS_{Res}}{n-k}}=(n-2)\dfrac{SS_{Reg}}{SS_{Res}}$$
여기서, $MS_{Reg}$는 회귀분산: 회귀집단의 분산
$MS_{Res}$는 잔차분산: 잔차집단내분산 $\because$ 회귀집단내분산=0
$SS_{Reg}$는 회귀변동
$SS_{Res}$는 잔차변동
$k$는 집단수: 회귀집단과 잔차집단 $\therefore k=2$
$n$은 표본크기
결정계수 = 설명된 변동 / 총 변동
$$R^2=\dfrac{SS_{Reg}}{SS_T}=\dfrac{SS_{Reg}}{SS_{Reg}+SS_{Res}}$$
여기서, $SS_{Reg}$는 회귀제곱합
$SS_{Res}$는 잔차제곱합
$SS_T$는 총제곱합
$SS_{Reg}$ / $SS_{Res}$
$$\dfrac{SS_{Reg}}{SS_{Res}}=\dfrac{R^2}{1-R^2}$$
$$\therefore F=(n-2)\dfrac{R^2}{1-R^2}$$
여기서, $n$은 표본크기
$R^2$은 결정계수
상관의 유의성
대응된 두 변수가 정규분포를 나타내는 확률변수이면 결정계수는 상관계수의 제곱
$$R^2 = r^2$$
$$F=(n-2)\dfrac{r^2}{1-r^2}$$
$$t=\sqrt{F}=\sqrt{(n-2)\dfrac{r^2}{1-r^2}}=\dfrac{r}{\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}}$$
여기서, $n$은 표본크기
$r$은 표본피어슨상관계수
상관분석표
| 변수 | 편차곱합 or 편차제곱합 | 자유도 | 편차곱평균 or 편차제곱평균 | 검정통계량 |
| $X,Y$ | $SM_{XY}$ | $n-1$ | $MM_{XY}=\dfrac{SM_{XY}}{n-1}=S_{XY}$ : $X$, $Y$의 표본공분산 | $$F=\dfrac{MS_{Reg}}{MS_{Res}}=(n-2)\dfrac{R^2}{1-R^2}∼F_{1,n-2}$$ 여기서, $R^2=\dfrac{s^2_{XY}}{s^2_{X}s^2_{Y}}$ |
| $X$ | $SS_X$ | $n-1$ | $MS_X=\dfrac{SS_X}{n-1}= S_X^2$ : $X$의 표본분산 | |
| $Y$ | $SS_X$ | $n-1$ | $MS_Y=\dfrac{SS_Y}{n-1}=S_Y^2$ : $Y$의 표본분산 |
상관분석 t검정표
| 귀무가설$(H_0)$ | 검정통계량 | 대립가설$(H_1)$ | 귀무가설 기각역 |
| $\rho=\rho_0$ | $$t=\dfrac{r-\rho_0}{\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}}$$ 여기서, $\rho_0$는 모상관계수 표본의 두 집단의 상관관계가 없으면 $\rho_0=0$ $r$은 표본상관계수 | $\rho<\rho_0$ | $t<-t_{n-2\ ;\ \alpha}$ |
| $\rho>\rho_0$ | $t>t_{n-2\ ;\ \alpha}$ | ||
| $\rho\neq \rho_0$ | $\mid{t}\mid>t_{n-2\ ;\ \frac{\alpha}{2}}$ |