확률분포 – Learning DATALINK

이산균등분포 – Discrete uniform distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k \, ; a, b)$

$K \sim U\{a,b\}$

$a$와 $b$

$a$와 $b$는 정수

$b \geq a$

$\therefore n=b-a+1$

$k \in \{a,a+1,\ldots, b-1,b\}$

$k$는 $a$이상이고 $b$이하인$k \in \{a,a+1,\ldots, b-1,b\}$

$k$는 $a$이상이고 $b$이하인 정수

$f(k \, ; a, b)=\dfrac{1}{n}$

for $a\leq k\leq b$

$f(k \, ; a, b)=0$

if not $a\leq k\leq b$

$\dfrac{e^{at}-e^{(b+1)^t}}{n(1-e^t)}$

평균 : $\dfrac{a+b}{2}$

분산 : $\dfrac{n^2-1}{12}$

$\mathrm{ln}(n)$

베르누이분포 – Bernoulli distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k ; p)$

$K \sim \text{Bern}(p)$

$p$

$p$는 성공확률

$0 < p < 1$

$q$는 실패확률

$q=1-p$

$k \in \{0, 1\}$

성공이면 $k=1$, 실패면 $k=0$

$f(k ; p) = p^k(1-p)^{(1-k)}$

$f(1 ; p)=\text{Pr}(K=1)=p$

$f(0 ; p)=\text{Pr}(K=0)=1-p$

이항(二項)분포 - Binomial distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k \, ; n,p)$

$K \sim \text{Bin}(n,p)$

$n$과 $p$

$n$은 시행횟수

$n \geq 0$

$p$는 성공확률

$0 \leq p \leq 1$

$q$는 실패확률

$q=1-p$

$k \in \{0, \ldots , n\}$

$k$는 성공횟수

$f(k \, ; n,p)=\dbinom{n}{k}p^k q^{n-k}$

$(1-p+pe^t)^n$

평균 : $np$

분산 : $npq$

$\dfrac{1}{2}\mathrm{ln}(2\pi nep(1-p))+O\left(\dfrac{1}{n}\right)$

음이항분포 - Negative Binomial distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

Method of moment

$f(k \, ; r,p)$

$K \sim \text{NB}(r,p)$

$r$과 $p$

$r$은 시행이 끝날 때까지 성공횟수

$r > 0$

$p$는 성공확률

$p \in [0,1]$

$k \in \{0,1,2,\ldots\}$

$k$는 실패할 때까지 시행횟수

$f(k \, ; r,p)=\dbinom{k+r-1}{k} (1-p)^r p^k$

$\left(\dfrac{1-p}{1-pe^t}\right)^r$

$\text{for} \ t<-\mathrm{log}p$

평균 : $\dfrac{pr}{1-p}$

분산 : $\dfrac{pr}{(1-p)^2}$

$r=\dfrac{{\rm E}[X]^2}{{\rm Var}[X]-E[X]}$

$p=1-\dfrac{{\rm E}[X]}{{\rm Var}[X]}$

초기하분포- Hypergeometric distribution

표기

Parameter

Support

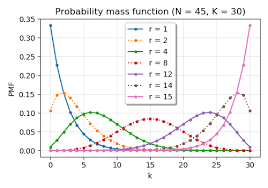
확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k \, ; N, K, n)$

$K \sim \text{Hyper}(N, K, n)$

$N$과 $K$와 $n$

$N$은 유한한 모집단의 크기

$N \in \{0,1,\ldots\} $

$K$는 모집단의 성공집단의 크기

$K \in \{0,1,\ldots,N\} $

$n$은 비복원추출 표본크기

$n \in \{0,1,\ldots,N\} $

$k \in \{\mathrm{max}(0, n+K=N),$

$\ldots ,\mathrm{min} (n,k)\}$

$k$는 표본에서 성공집단의 크기

$f(k \, ; N, K, n)=\dfrac{\dbinom{K}{k}\dbinom{N-K}{n-k}}{\dbinom{N}{n}}$

$\dfrac{\dbinom{N-K}{n} \sideset{_2}{_1}F(-n,-K;N-K-n+1:e^t)}{\dbinom{N}{n}}$

평균 : $n\dfrac{K}{N}$

분산 : $n\dfrac{K}{N}\dfrac{N-K}{N}\dfrac{N-n}{N-1}$

음초기하분포- Negative Hypergeometric distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k \, ; N, K, r)$

$K \sim \text{NH}(N, K, r)$

$N$과 $K$와 $r$

$N$은 유한한 모집단의 크기

$N \in \{0,1,\ldots\} $

$K$는 모집단의 성공집단의 크기

$K \in \{0,1,\ldots,N\} $

$r$은 표본의 기대 성공집단의 크기

$r \in \{0,1,\ldots,N\} $

$k \in \{\mathrm{max}(0, r+K=N),$

$\ldots ,\mathrm{min} (k,r)\}$

$k$는 비복원추출 표본크기

$f(k \, ; N, K, r)=\dfrac{\dbinom{k-1}{r-1}\dbinom{N-k}{K-r}}{\dbinom{N}{K}}$

$\dfrac{\dbinom{N-K}{r} \sideset{_2}{_1}F(-r,-K;N-K-r+1:e^t)}{\dbinom{N}{K}}$

평균 : $k\dfrac{N}{K}$

분산 : $r\dfrac{K}{N}\dfrac{N-K}{N}\dfrac{N-r}{K}$

기하분포 - Geometric distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k \, ; p)$

$K \sim \text{Geom}(p)$

$p$

$p$는 성공확률

$0＜ p ≤ 1$

$k\in \{1,2,\ldots\}$

$k$는 실패할 때까지 시행횟수

$f(k \, ; p)=(1-p)^{k-1}p$

$\dfrac{pe^t}{1-(1-p)e^t}$

여기서, $t < \mathrm{ln}(1-p)$

평균 : $\dfrac{1}{p}$

분산 : $\dfrac{1-p}{p^2}$

$\dfrac{-(1-p)\mathrm{log}_2 (1-p)-p\ \mathrm{log}_2 p}{p}$

포아송분포 - Poisson distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(k \, ; \lambda)$

$K \sim \text{Poisson}(\lambda)$

$\lambda$

$\lambda$는 단위시간 또는 단위공간에서 발생하는 사건발생 평균횟수: rate

$\lambda \in (0,\infty)$

$k \in \{0,1,2,\ldots\}$

$k$는 사건발생 횟수

$f(k \, ; \lambda)=\dfrac{\lambda^k e^{-\lambda}}{k!}$

$\mathrm{exp}(\lambda(e^t -1))$

평균 : $\lambda$

분산 : $\lambda$

$\lambda[1-\mathrm{log}(\lambda)]+e^{-\lambda}\sum_{k=0}^{\infty}\dfrac{\lambda^k\mathrm{log}(k!)}{k!}$

다항분포 - Multinomial distribution

표기

Parameter

Support

확률분포도

확률질량함수

모멘트생성함수

엔트로피

$f(x_i \, ; n,p_i)$

$(X_1, X_2, \dots, X_k) \sim$

$\text{Multinomial}(n; p_1, p_2, \dots, p_k)$

$n$과 $k$와 $p_k$

$n$은 시행횟수

$n$은 $0$과 자연수

$k$는 독립시행 수

$k$는 $0$과 자연수

$p_k$는 $k$번째 시행에서의 확률질량

$p_k \in \{ p_1, \ldots, p_n \}$

$\sum_\limits{k=1}^{n} p_k=1$

$x_i \in\{x_1, \ldots x_{k} \}$

$\sum\limits_{i}^{k} x_{i}=n$

$f(x_i \, ; n,p_i)=\dfrac{n!}{x_1! \cdots x_k!}p_1^{x_1} \cdots p_k^{x_k}$

$\left(\sum_{i=1}^{k}p_i e^{t_i}\right)^n$

평균 : ${\operatorname {E}}[X_i]=n{p_i}$

분산 : ${\operatorname {Var}}(X_i)=n{p_i}(1-p_i)$

${\operatorname {Cov}}(X_i,X_j)=-n{p_i}{p_j}\ \ (i\neq j)$

$-\mathrm{log}(n!)-n\sum_{i=1}^{k}p_i\mathrm{log}(p_i)+$

$\sum_{i=1}^{k} \sum_{x_i=0}^{n} \dbinom{n}{x_i}p_i^{x_i} (1-p_i)^{n-x_i}\mathrm{log}(x_i !)$

연속균등분포 – Continuous uniform distribution

표기

Parameter

Support

확률분포도

확률밀도함수(f) - 누적분포함수(F)

모멘트생성함수

엔트로피

$f(x \, ; a, b)$

$X \sim U(a,b)$

$a$와 $b$

$a$와 $b$는 실수

$ a < b $

$x \in [a, b]$

$f(x \, ; a, b)=\dfrac{1}{(b-a)}$

for $a ≤ x ≤ b$

$f(x \, ; a, b)=0$

for $x < a $ or $x > b$

$F(x \, ; a, b)=0$

for $x < a$

$$F(x \, ; a, b)=\dfrac{x-a}{b-a}$$

for $a < x < b$

$$F(x \, ; a, b)=1$$

for $b < x$

$\dfrac{e^{tb}-e^{ta}}{t(b-a)}$

평균 : $\dfrac{1}{2}(a+b)$

분산 : $\dfrac{1}{12}(b-a)^2$

$\mathrm{ln}(b-a)$

지수분포 – Exponential distribution

표기

Parameter

Support

확률분포도

확률밀도함수(f) - 누적분포함수(F)

모멘트생성함수

엔트로피

$f(x \, ; \lambda)$

$X \sim \text{Exp}(\lambda)$

$\lambda$

$\lambda$는 rate, inverse scale

$\lambda$는 양의실수

$x \in [0, +\infty)$

$f(x \, ; \lambda)=\lambda e^{-\lambda x}=\lambda \left(\dfrac{1}{e}\right)^{\lambda x}$

for $x ≥ 0$

$f(x \, ; \lambda)=0$

for $x < 0$

$F(x \, ; \lambda)=1-e^{-\lambda x}=1-\left(\dfrac{1}{e}\right)^{\lambda x}$

for $x ≥ 0$

$F(x \, ; \lambda)=0$

for $x < 0$

$\dfrac{\lambda}{\lambda -t} \,\, \ \text{for} \ t<\lambda$

평균 : $\dfrac{1}{\lambda}$

분산 : $\dfrac{1}{\lambda^2}$

$1-\ln \lambda$

정규분포 – Normal distribution

표기

Parameter

Support

확률분포도

확률밀도함수(f) - 누적분포함수(F)

모멘트생성함수

엔트로피

$f(x \, ; \mu, \sigma_X^2)$

$X \sim N(\mu, \sigma^2)$

$\mu$와 $\sigma^2$

$\mu$는 평균

$\mu$는 실수

$\mu$는 location

$\sigma^2$은 분산

$\sigma^2$은 양의 실수

$\sigma^2$은 squared scale

$x\in[-\infty, +\infty]$

$f(x \, ; \mu, \sigma^2)=\dfrac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

$F(x \, ; \mu, \sigma^2)=\dfrac{1}{2}\left(1+\operatorname {erf}\left(\dfrac{x-\mu}{\sqrt{2}\sigma}\right)\right)$

여기서, $\operatorname {erf} (x)=\dfrac {2}{\sqrt {\pi }}\int _{0}^{x}e^{-t^2}\,dt$

$M_X (t)=\mathrm{exp}\left(\mu t+\dfrac{\sigma^2 t^2}{2}\right)$

평균 : $\mu$

분산 : $\sigma^2$

$12\ln(2πσ^2)+12$

베타분포 – Beta distribution

표기

Parameter

Support

확률분포도

확률밀도함수

모멘트생성함수

엔트로피

$f(x \, ; \alpha, \beta)$

$X \sim \text{Beta}(\alpha, \beta)$

$\alpha$와 $\beta$

$\alpha$는 shape

$\alpha$는 양의 실수

$\beta$는 shape

$\beta$는 양의 실수

$x \in [0, 1]$

$f(x \, ; \alpha, \beta)=\dfrac {x^{\alpha -1}(1-x)^{\beta -1}}{B (\alpha ,\beta)}$

여기서, $B$는 베타함수:

$B(\alpha ,\beta )=\dfrac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}$

여기서, $\Gamma(\alpha)$는 감마함수로, $\alpha$가 정수일 경우 $ (\alpha-1)! $와 동일

$1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}$

평균 :

$\mathrm {E} [X]=\dfrac{\alpha}{\alpha +\beta}$

$$\mathrm {E} [\ln X]=\psi (\alpha )-\psi (\alpha +\beta)$$

분산 :

$ \mathrm {Var} (X)={\dfrac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}$

$\mathrm {Var} (\ln X)=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )$

$\ln \mathrm {B} (\alpha ,\beta )-(\alpha -1)\psi (\alpha )$

$-(\beta -1)\psi (\beta )$

$+(\alpha +\beta -2)\psi (\alpha +\beta )$

감마분포 – Gamma distribution

표기

Parameter

Support

확률분포도

확률밀도함수

모멘트생성함수

엔트로피

$f(x \, ; k,\theta)$

$X \sim \text{Gamma}(k,\theta)$

$f(x \, ; \alpha, \beta)$

$X \sim \text{Gamma}(\alpha, \beta)$

$k$와 $\theta$

$k$는 shape

$k$는 양의 실수

$$k=\dfrac{{\rm E}[X]^{2}}{{\rm Var}[X]}$$

$\theta$는 shape

$\theta$는 양의 실수

$$ \theta =\dfrac{{\rm Var}[X]}{{\rm E}[X]}$$

$\alpha$와 $\beta$

$\alpha$는 shape

$\alpha$는 양의 실수

$$\alpha=\dfrac{{\rm E}[X]^{2}}{{\rm Var}[X]}$$

$\beta$는 shape

$\beta$는 양의 실수

$$\beta =\dfrac{{\rm E}[X]}{{\rm Var}[X]}$$

$x∈(0,+\infty)$

$f(x \, ; k,\theta)=x^{k-1}\dfrac{\mathrm{exp}\left(\frac{-x}{\theta}\right)}{\Gamma (k)\theta^k}$

$f(x \, ; \alpha, \beta)={\dfrac{\beta ^{\alpha }}{\Gamma (\alpha )}}x^{\alpha -1}e^{-\beta x}$

여기서, $\Gamma(\alpha)$는 감마함수로, $\alpha$가 정수일 경우 $ (\alpha-1)! $와 동일

$(1-\theta t)^{-k} \ \text{for} \ t < \dfrac{1}{\theta}$

평균 : $k\theta$

분산 : $k\theta^2$

$ \left(1-\dfrac{t}{\beta}\right)^{-\alpha } \ \text{for} \ t<\beta$

평균 : $\dfrac{\alpha}{\beta}$

분산 : $\dfrac{\alpha}{\beta^2}$

$k + \ln\theta+\ln\Gamma(k)+(1-k)\psi(k)$

$\alpha + \ln\beta+\ln\Gamma(\alpha)+(1-\alpha)\psi(\alpha)$

카이제곱($\chi^2$)분포 – Chi-squared distribution

표기

Parameter

Support

확률분포도

확률밀도함수

모멘트생성함수

엔트로피

$f(x \, ; k)$

$X \sim \chi^2(k)$

$X \sim \chi_k^2$

$k$

$k$는 자유도

$k$는 양의 실수

$x \in (0, +\infty)$

$k=1$인 경우

$x \in [0, +\infty)$

$k≠1$인 경우

$f(x \, ; k)=\dfrac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}$

$(1-2t)^{\frac{-k}{2}}$

for $t<\dfrac{1}{2}$

평균 : $k$

분산 : $2k$

$\dfrac{k}{2}+\mathrm{ln}\left(2\Gamma\left(\dfrac{k}{2}\right)\right)+\left(1-\dfrac{k}{2}\right)\psi\left(\dfrac{k}{2}\right)$

t분포 - Student t distribution

표기

Parameter

Support와 확률변수 변환식

확률분포도

확률밀도함수

모멘트생성함수

엔트로피

$f(t \, ; \nu)$

$T \sim t(\nu)$

$T \sim t_{\nu}$

$\nu$

$\nu$는 자유도(degree of freedom)

$t \in (-\infty, +\infty)$

$t=\dfrac{z}{\sqrt {\dfrac{V}{\nu}}}=\dfrac {{\bar {x}}-\mu }{\dfrac{s}{\sqrt {n}}}$

여기서, $t$는 t분포를 나타내는 확률변수

$z$는 표준정규분포함수

$V$는 카이제곱

$\nu$는 자유도

$s$는 표본표준편차

$\bar x$는 표본평균

$n$은 표본크기

$f(t \, ; \nu)= \frac{\Gamma\left(\frac{\nu + 1}{2}\right)}{\sqrt{\nu \pi} \Gamma\left(\frac{\nu}{2}\right)} \left(1 + \frac{t^2}{\nu}\right)^{-\frac{\nu + 1}{2}}
$

여기서, $\nu$는 자유도

$\Gamma( \,\,)$는 감마함수

$M_{X}(t)$는 없음

평균 : $0$

for $\nu >1$

분산 : $\dfrac{\nu}{\nu-2}$

for $\nu >2$

분산 : $\infty$

for $1 < \nu ≤ 2$

$\dfrac{\nu +1}{2}\left[\psi \left(\dfrac{1+\nu}{2}\right)-\psi \left(\dfrac{\nu}{2}\right)\right]$

$+\ln \left[\sqrt{\nu}{\rm B}\left(\dfrac{\nu}{2},\dfrac{1}{2}\right)\right]$

여기서, $\psi$는 digamma function

$\rm B$는 beta function

F분포 – F distribution

표기

Parameter와 확률변수

Support와 확률변수 변환식

확률분포도

확률밀도함수

모멘트생성함수

엔트로피

$f(x \, ; d_1, d_2)$

$X \sim F(d_1, d_2)$

$X \sim F_{d_1, d_2}$

$d_1$과 $d_2$

$d_1$과 $d_2$는 자유도

$d_1$과 $d_2$는 양의 실수

$x \in (0, +\infty)$

$d_1=1$인 경우

$x \in [0, +\infty)$

$d_1≠1$인 경우

$X=\dfrac{V_1}{d_1} \div \dfrac{V_2}{d_2}$

$x={\dfrac {s_{1}^{2}}{\sigma _{1}^{2}}}\div {\dfrac {s_{2}^{2}}{\sigma _{2}^{2}}}$

여기서, $X$는 F분포를 나타내는 확률변수

$x$는 확률변수값

$V_1$과 $V_2$는 집단1과 집단2의 $\chi^2$

$f(x; d_1, d_2) = \frac{\Gamma(\frac{d_1 + d_2}{2})}{\Gamma(\frac{d_1}{2})\Gamma(\frac{d_2}{2})} \left(\frac{d_1}{d_2}\right)^{\frac{d_1}{2}}$

$\cdot x^{\frac{d_1}{2} – 1} \left(1 + \frac{d_1}{d_2}x\right)^{-\frac{d_1 + d_2}{2}}$

여기서, $d_1$과 $d_2$는 각각 분자와 분모의 자유도

$\Gamma(\,\,)$는 감마함수

$M_{X}(t)$는 없음

평균 :

$\dfrac{d_2}{d_2-2}$

for $d_2 > 2$

분산 :

$\dfrac{{2d_2^2}({d_1}+{d_2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}$

for $d_2 >4$

$\ln \Gamma \left({\tfrac {d_{1}}{2}}\right)+\ln \Gamma \left({\tfrac {d_{2}}{2}}\right)-\ln \Gamma \left({\tfrac {d_{1}+d_{2}}{2}}\right)$

$\cdot \left(1-{\tfrac {d_{1}}{2}}\right)\psi \left(1+{\tfrac {d_{1}}{2}}\right)$

$-\left(1+{\tfrac {d_{2}}{2}}\right)\psi \left(1+{\tfrac {d_{2}}{2}}\right)$

$+\left({\tfrac {d_{1}+d_{2}}{2}}\right)\psi \left({\tfrac {d_{1}+d_{2}}{2}}\right)+\ln {\frac {d_{1}}{d_{2}}}$

다변량정규분포 – Multivariate normal distribution

표기

Parameter

Support

확률분포도

확률밀도함수

모멘트생성함수

엔트로피

$f(\boldsymbol {x} \, ; \boldsymbol {\mu} , \boldsymbol {\Sigma})$

$X \sim \mathcal{N}(\boldsymbol{\mu}, \, \boldsymbol{\Sigma})$

$\boldsymbol{\mu}$와 $\boldsymbol\Sigma$

$\boldsymbol{\mu}$는 평균

$$\boldsymbol{\mu} \in \Bbb{R}^k $$

$\boldsymbol\Sigma$는 공분산행렬

$\boldsymbol\Sigma \in \Bbb{R}^{k \times k}$

$\boldsymbol {x} \in \boldsymbol \mu +\text{span}(\boldsymbol \Sigma)\subseteq \Bbb{R}^k$

$f(\boldsymbol {x} \, ; \boldsymbol {\mu} , \boldsymbol {\Sigma})=(2\pi )^{-k/2}\det({\boldsymbol {\Sigma }})^{-1/2}$

$\cdot \exp \left(-{\frac {1}{2}}(\mathbf {x} -{\boldsymbol {\mu }})^{\!{\mathsf {T}}}{\boldsymbol {\Sigma }}^{-1}(\mathbf {x} -{\boldsymbol {\mu }})\right)$

$\boldsymbol{\Sigma}$가 positive-define일 때만 존재

$\mathrm{exp}\left(\boldsymbol{\mu}^{\mathsf{T}}{\boldsymbol{t}}+\dfrac{1}{2}\boldsymbol{t}^{\mathsf{T}}\boldsymbol{\Sigma} \boldsymbol{t}\right)$

평균 : $\boldsymbol {\mu}$

분산 : $\boldsymbol \Sigma$

$\dfrac{1}{2} \ln \det \left(2\pi \mathrm {e} \boldsymbol {\Sigma}\right)$