프로그래밍
구글시트
데이터
수집, 시각화, 설명
모델링
확률모델, 새 확률변수, 통계모델, 연구계획
데이터분석
모수추정, 모수비교
표본종류: 대응표본
확률변수가정: 정규성, 두 변수는 선형관계
새확률변수: 상관계수(공분산/표준편차곱)
표집분포: 상관계수 중심극한정리
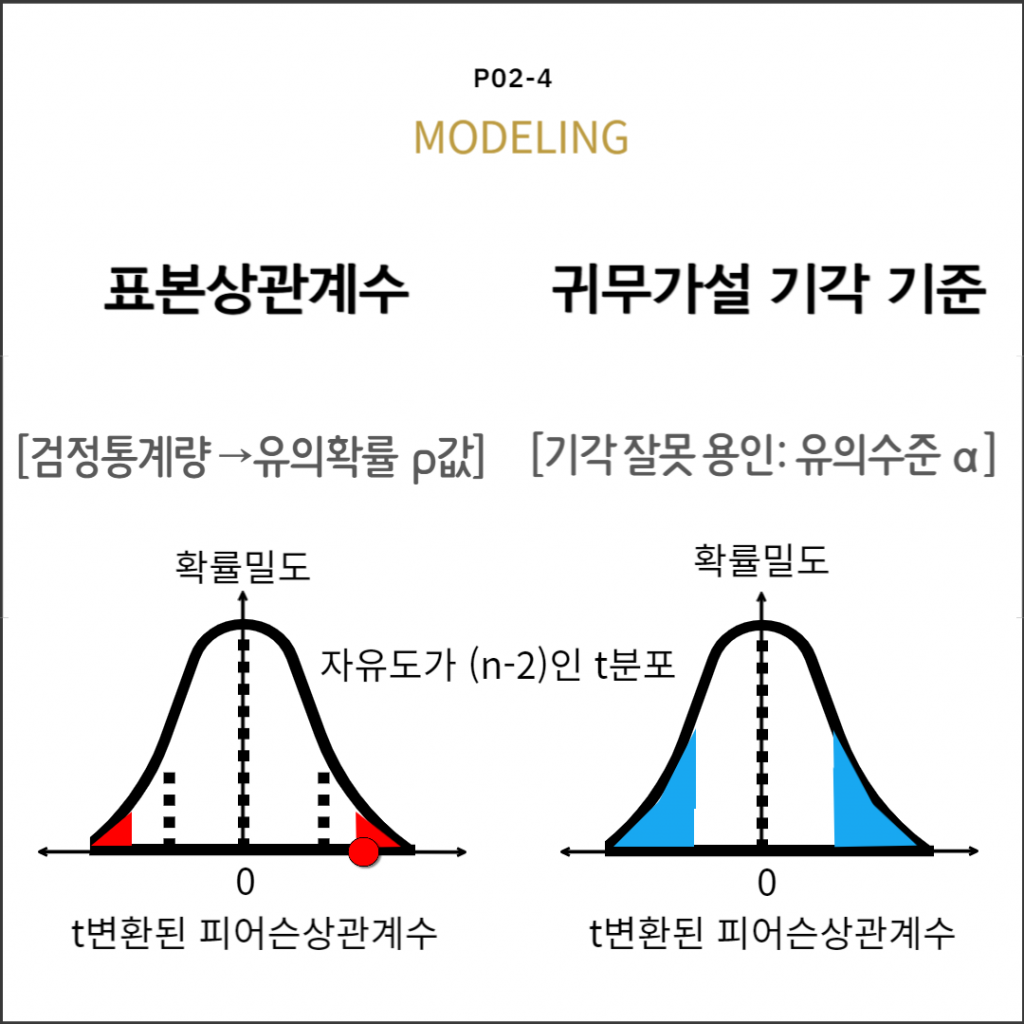
검정확률분포: t분포
검정통계량: 표본상관계수와 표준오차의 비
귀무가설: 마스와 등지함의 상관계수는 0
가설검정: 유의확률과 유의수준을 비교
정규분포
$$f(y \, ; \mu_Y, \sigma_Y^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right)$$
여기서, $y$는 정규분포를 나타내는 확률변수, $Y$의 값(변량)
$\mu_Y$는 확률변수, $Y$의 기대값: 집단의 모평균
$\sigma_Y^2$는 확률변수, $Y$의 모분산: 집단의 모분산
확률변수 t
$$t = \dfrac{Z}{\sqrt{\dfrac{V} {\nu}}}$$
여기서, $Z$는 표준정규분포를 나타내는 확률변수
$V$는 자유도 $\nu$의 $\chi^2$분포를 나타내는 확률변수
$\nu$는 $V$의 자유도
t분포
$$f(t \, ; \nu)=\dfrac{\Gamma \left({\frac{\nu +1}{2}}\right)}{\sqrt{\nu \pi}\Gamma \left(\dfrac{\nu }{2}\right)}\left(1+\dfrac {t^2}{\nu }\right)^{-\frac{\nu +1}{2}}$$
여기서, $t$는 t분포를 나타내는 확률변수
$\nu$는 자유도
$\Gamma(\,\,)$는 감마함수
F = 집단간분산 / 집단내분산
$$F=\dfrac{MS_{B}}{MS_{W}}=\dfrac{\dfrac{SS_{B}}{k-1}}{\dfrac{SS_{W}}{n-k}}$$
여기서, $MS_B$는 집단간분산
$MS_W$는 집단내분산
$SS_B$는 집단간변동
$SS_W$는 집단내변동
$k$는 집단수
$n$은 표본크기
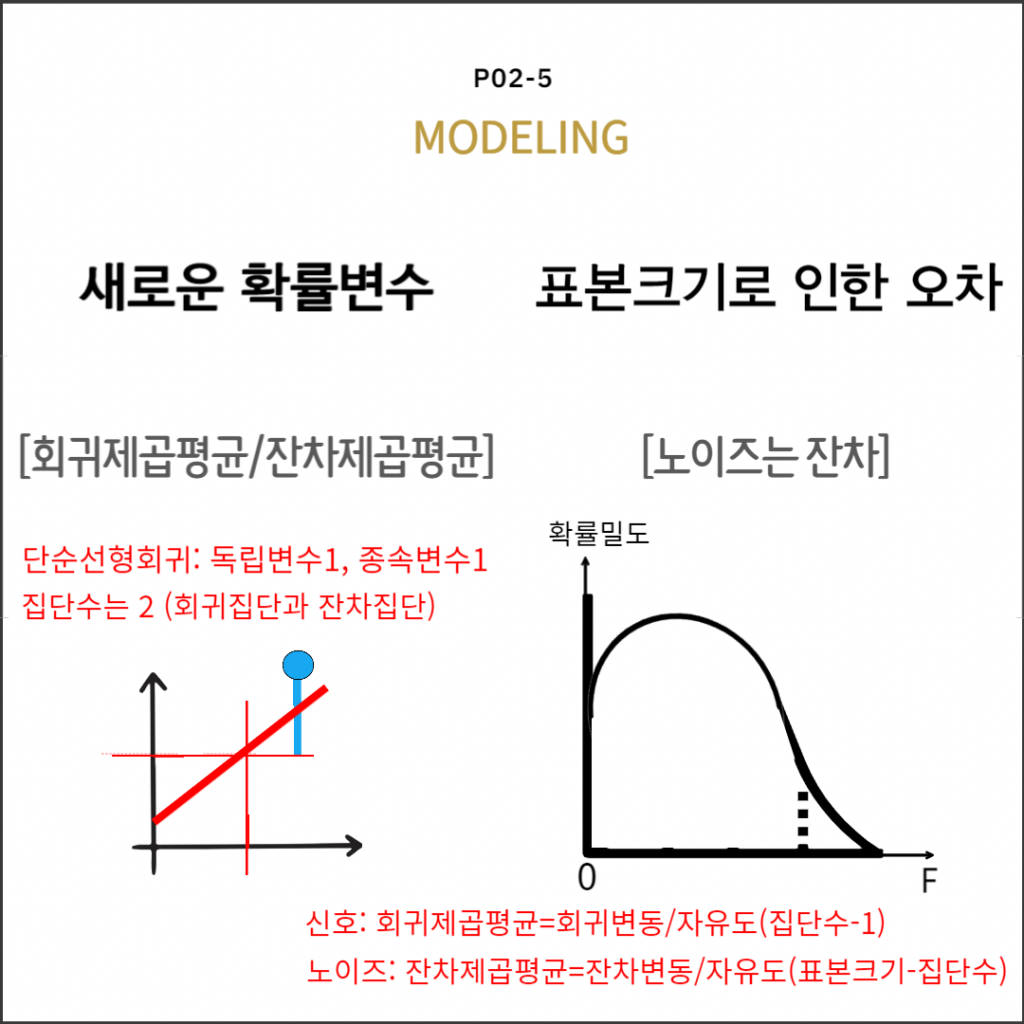
F = 회귀분산 / 잔차분산
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{SS_{Reg}}{k-1}}{\dfrac{SS_{Res}}{n-k}}=(n-2)\dfrac{SS_{Reg}}{SS_{Res}}$$
여기서, $MS_{Reg}$는 회귀분산: 회귀집단의 분산
$MS_{Res}$는 잔차분산: 잔차집단내분산 $\because$ 회귀집단내분산=0
$SS_{Reg}$는 회귀변동
$SS_{Res}$는 잔차변동
$k$는 집단수: 회귀집단과 잔차집단 $\therefore k=2$
$n$은 표본크기
결정계수 = 설명된 변동 / 총 변동
$$R^2=\dfrac{SS_{Reg}}{SS_T}=\dfrac{SS_{Reg}}{SS_{Reg}+SS_{Res}}$$
여기서, $SS_{Reg}$는 회귀제곱합
$SS_{Res}$는 잔차제곱합
$SS_T$는 총제곱합
$SS_{Reg}$ / $SS_{Res}$
$$\dfrac{SS_{Reg}}{SS_{Res}}=\dfrac{R^2}{1-R^2}$$
$$\therefore F=(n-2)\dfrac{R^2}{1-R^2}$$
여기서, $n$은 표본크기
$R^2$은 결정계수
상관의 유의성
대응된 두 변수가 정규분포를 나타내는 확률변수이면 결정계수는 상관계수의 제곱
$$R^2 = r^2$$
$$F=(n-2)\dfrac{r^2}{1-r^2}$$
$$t=\sqrt{F}=\sqrt{(n-2)\dfrac{r^2}{1-r^2}}=\dfrac{r}{\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}}$$
여기서, $n$은 표본크기
$r$은 표본피어슨상관계수
상관분석표
| 변수 | 편차곱합 or 편차제곱합 | 자유도 | 편차곱평균 or 편차제곱평균 | 검정통계량 |
| $X,Y$ | $SM_{XY}$ | $n-1$ | $MM_{XY}=\dfrac{SM_{XY}}{n-1}=S_{XY}$ : $X$, $Y$의 표본공분산 | $$F=\dfrac{MS_{Reg}}{MS_{Res}}=(n-2)\dfrac{R^2}{1-R^2}∼F_{1,n-2}$$ 여기서, $R^2=\dfrac{s^2_{XY}}{s^2_{X}s^2_{Y}}$ |
| $X$ | $SS_X$ | $n-1$ | $MS_X=\dfrac{SS_X}{n-1}= S_X^2$ : $X$의 표본분산 | |
| $Y$ | $SS_X$ | $n-1$ | $MS_Y=\dfrac{SS_Y}{n-1}=S_Y^2$ : $Y$의 표본분산 |
상관분석 t검정표
| 귀무가설$(H_0)$ | 검정통계량 | 대립가설$(H_1)$ | 귀무가설 기각역 |
| $\rho=\rho_0$ | $$t=\dfrac{r-\rho_0}{\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}}$$ 여기서, $\rho_0$는 모상관계수 표본의 두 집단의 상관관계가 없으면 $\rho_0=0$ $r$은 표본상관계수 | $\rho<\rho_0$ | $t<-t_{n-2\ ;\ \alpha}$ |
| $\rho>\rho_0$ | $t>t_{n-2\ ;\ \alpha}$ | ||
| $\rho\neq \rho_0$ | $\mid{t}\mid>t_{n-2\ ;\ \frac{\alpha}{2}}$ |
표본종류: 대응표본
확률변수가정: 두 변수의 선형성, 잔차의 등분산성, 독립성, 정규성
새확률변수: 결정계수(공분산제곱과 분산곱의 비)
표집분포: 결정계수 중심극한정리
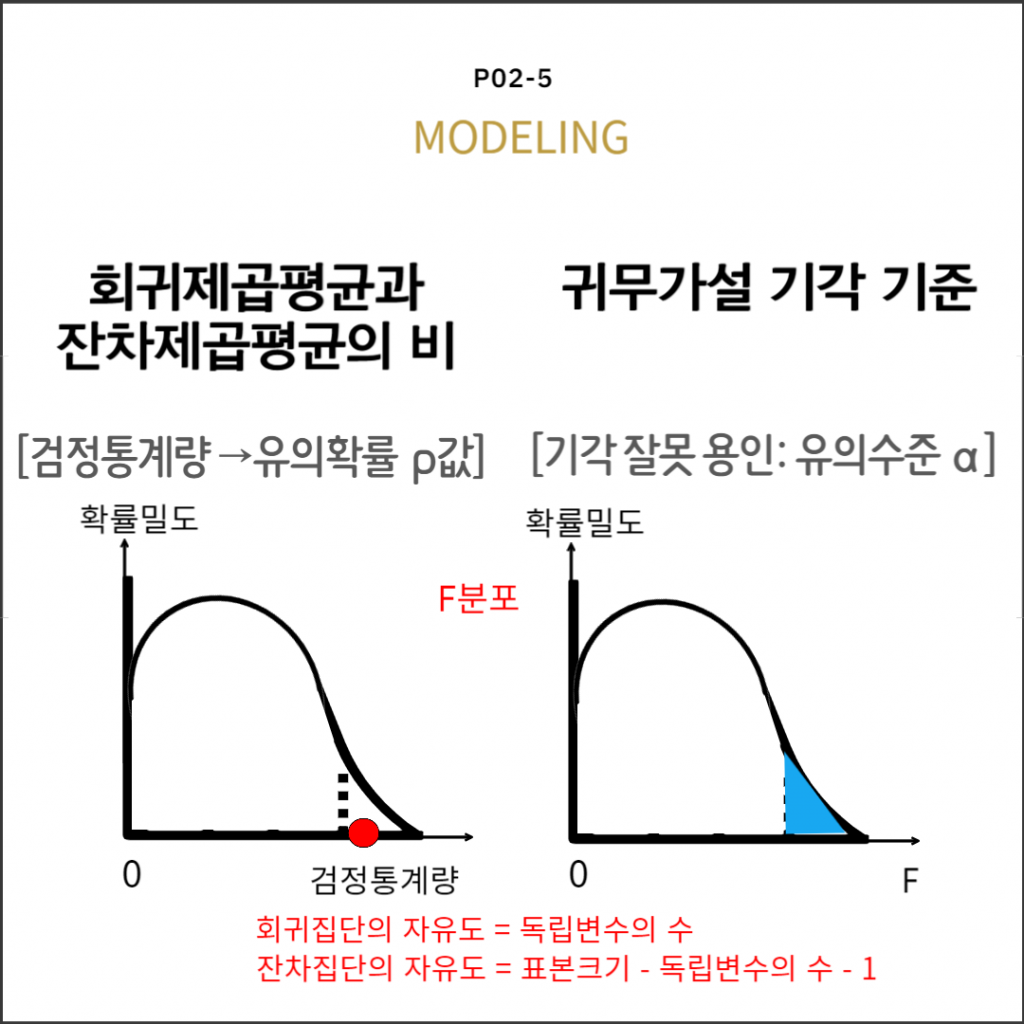
검정확률분포: F분포
검정통계량: 표본결정계수와 표준오차의 비
귀무가설: 마스로 설명되는 등지함은 0
가설검정: 유의확률과 유의수준을 비교
정규분포
$$f(y \, ; \mu_Y, \sigma_Y^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right)$$
여기서, $y$는 정규분포를 나타내는 확률변수, $Y$의 값(변량)
$\mu_Y$는 확률변수, $Y$의 기대값: 집단의 모평균
$\sigma_Y^2$는 확률변수, $Y$의 모분산: 집단의 모분산
확률변수 카이제곱
$$\chi^2= Z_1^2 + Z_2^2 + \cdots = \sum\limits_{i=1}^{k}Z_{i}^2$$
여기서, $Z_i$는 표준정규분포 확률변수
$k$는 자유도: 표준정규분포 확률변수 개수
카이제곱분포
$$f(x \, ; k)=\dfrac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}$$
여기서, $x$는 카이제곱분포를 나타내는 확률변수의 값(변량)
$k$는 자유도: 확률변수제곱의 개수
확률변수 F
$$F = \dfrac{\frac{\chi^2_1}{d_1}}{\frac{\chi^2_2}{d_2}}$$
여기서, $F$는 F분포를 나타내는 확률변수
$\chi^2_1$과 $\chi^2_2$는 카이제곱분포를 나타내는 확률변수
$d_1$과 $d_2$는 $\chi^2_1$과 $\chi^2_2$가 나타내는 카이제곱분포의 자유도
F분포
$$f(x; d_1, d_2) = \frac{\left(\dfrac{d_1}{d_2}\right)^{\frac{d_1}{2}} x^{\frac{d_1}{2} – 1} \left(1 + \frac{d_1}{d_2}x\right)^{-\frac{d_1 + d_2}{2}}}{B\left(\frac{d_1}{2}, \frac{d_2}{2}\right)}
$$
여기서, $x$는 F분포를 나타내는 확률변수의 값(변량)
$d_1$과 $d_2$는 각각 분자와 분모의 자유도
$B(\,\,)$는 베타함수
$B(\frac{d_1}{2}, \frac{d_2}{2}) = \frac{\Gamma(\frac{d_1}{2}) \Gamma(\frac{d_2}{2})}{\Gamma(\frac{d_1}{2} + \frac{d_2}{2})}$
$\Gamma(\,\,)$는 감마함수
F = 집단간분산 / 집단내분산
$$F=\dfrac{MS_{B}}{MS_{W}}=\dfrac{\dfrac{SS_{B}}{k-1}}{\dfrac{SS_{W}}{n-k}}$$
여기서, $MS_B$는 집단간분산
$MS_W$는 집단내분산
$SS_B$는 집단간변동
$SS_W$는 집단내변동
$k$는 집단수
$n$은 표본크기
F = 회귀분산 / 잔차분산
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{SS_{Reg}}{k-1}}{\dfrac{SS_{Res}}{n-k}}=(n-2)\dfrac{SS_{Reg}}{SS_{Res}}$$
여기서, $MS_{Reg}$는 회귀분산: 회귀집단의 분산
$MS_{Res}$는 잔차분산: 잔차집단내분산 $\because$ 회귀집단내분산=0
$SS_{Reg}$는 회귀변동
$SS_{Res}$는 잔차변동
$k$는 집단수: 회귀집단과 잔차집단 $\therefore k=2$
$n$은 표본크기
결정계수 = 설명된 변동 / 총 변동
$$R^2=\dfrac{SS_{Reg}}{SS_T}=\dfrac{SS_{Reg}}{SS_{Reg}+SS_{Res}}$$
여기서, $SS_{Reg}$는 회귀제곱합
$SS_{Res}$는 잔차제곱합
$SS_T$는 총제곱합
$SS_{Reg}$ / $SS_{Res}$
$$\dfrac{SS_{Reg}}{SS_{Res}}=\dfrac{R^2}{1-R^2}$$
$$F=(n-2)\dfrac{R^2}{1-R^2}$$
여기서, $n$은 표본크기
$R^2$은 결정계수
회귀직선의 적합성
$$R^2=r^2$$
$$F=(n-2)\dfrac{r^2}{1-r^2}$$
여기서, $n$은 표본크기
$r$은 표본피어슨상관계수
단순선형회귀분석표
| 변동: 편차제곱합 | 자유도 | 분산: 편차제곱평균 | 검정통계량 | |
| 회귀 (Regression) | $SS_{Reg}$ | $1$ | ${MS}_{Reg}=\dfrac{SS_{Reg}}{1}$ | $F=\dfrac{MS_{Reg}}{MS_{Res}}=(n-2)\dfrac{SS_{Reg}}{SS_{Res}}$ |
| 잔차 (Residual) | $SS_{Res}$ | $n-2$ | $MS_{Res}=\dfrac{SS_{Res}}{n-2}$ | |
| 벡터합 (Total) | $SS_T$ | $n-1$ | $MS_T=\dfrac{SS_T}{n-1}$ |
단순선형회귀분석 F검정표
| 귀무가설$(H_0)$ | 검정통계량 | 대립가설$(H_1)$ | 귀무가설 기각역 |
| $$ \beta_1=\beta_{1,0}$$ | $F=\dfrac{MS_{Reg}}{MS_{Res}}$ | $\beta_1<\beta_{1,0}$ | 검정통계량으로 $\beta_1$이 $\beta_{1,0}$보다 작은 지 알 수 없다. |
| $\beta_1>\beta_{1,0}$ | 검정통계량으로 $\beta_1$이 $\beta_{1,0}$보다 큰 지 알 수 없다. | ||
| $$ \beta_1 \ne \beta_{1,0}$$ | $F\gt F_{1,\ n-2\ ;\ \alpha}$ |
표본종류: 대응표본
등분산성, 독립성, 정규성, 선형성
새확률변수: 각 Cell의 표본확률차이의 합
표집분포: 표본카이제곱 중심극한정리
검정확률분포: 카이제곱분포
검정통계량: 표본카이제곱과 표준오차의 비
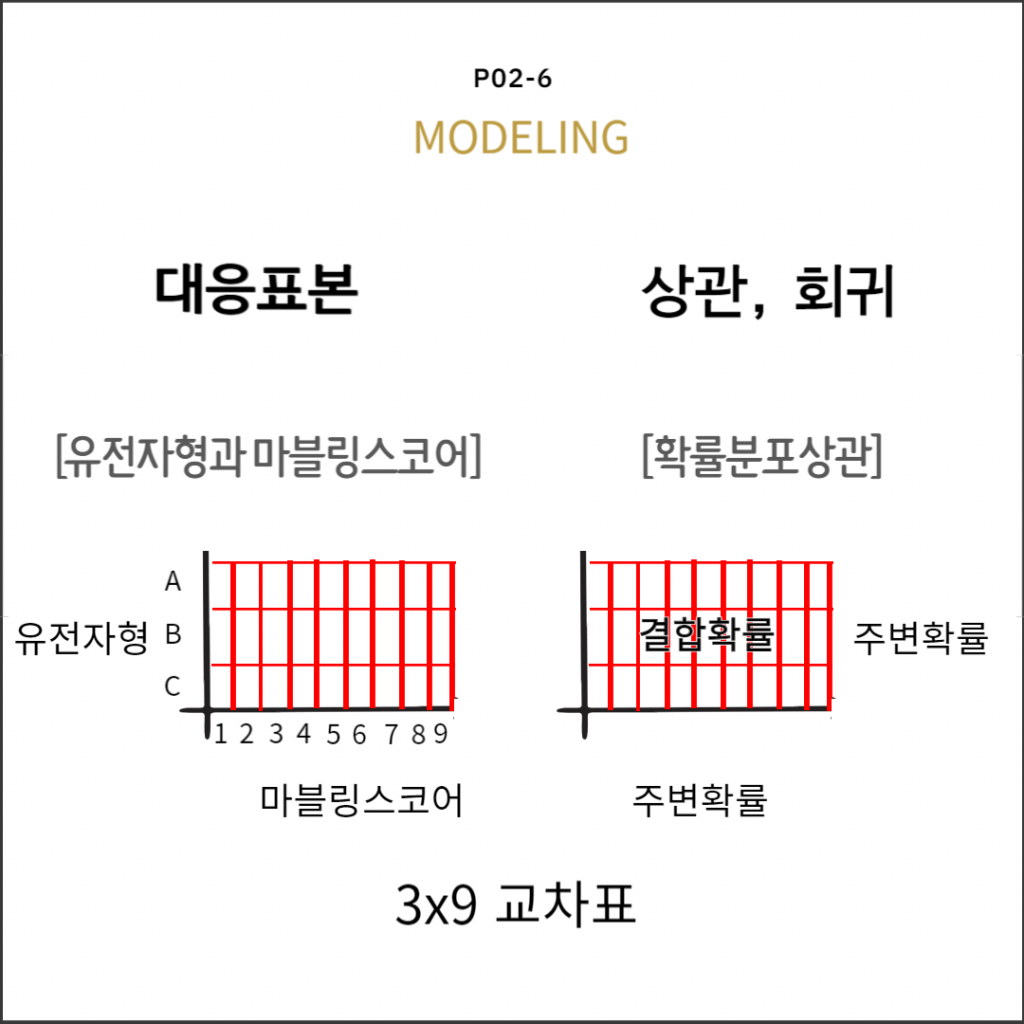
귀무가설: 유전자형에 따른 마스의 확률분포는 같다.
가설검정: 유의확률과 유의수준을 비교
정규분포
$$f(x \, ; \mu_X, \sigma_X^2)=\dfrac{1}{\sqrt{2\pi}\sigma_X} \mathrm{exp} \left(-\dfrac{(x-\mu_X)^2}{2\sigma_X^2}\right)$$
여기서, $x$는 정규분포를 나타내는 확률변수, $X$의 값(변량)
$\mu_X$는 확률변수, $X$의 기대값: 집단의 모평균
$\sigma_X^2$는 확률변수, $X$의 모분산: 집단의 모분산
확률변수 카이제곱
$$\chi^2= Z_1^2 + Z_2^2 + \cdots = \sum\limits_{i=1}^{k}Z_{i}^2$$
여기서, $Z_i$는 표준정규분포 확률변수
$k$는 자유도: 표준정규분포 확률변수 개수
카이제곱분포
$$f(x \, ; k)=\dfrac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}$$
여기서, $x$는 카이제곱분포를 나타내는 확률변수의 값(변량)
$k$는 자유도: 확률변수제곱의 개수
기대빈도수 산출
관측빈도수 표집분포
$i$행과 $j$열로 구분되는 범주(집단)에서의 관측빈도수를 $O_{ij}$로 표기하고 기대빈도수를 $E_{ij}$로 표기합니다. 표본크기($N$)가 큰 경우, 관측빈도수($O_{ij}$)의 표집분포는 중심극한정리에 의해 기대빈도수($E_{ij}$)를 평균으로 하고 $E_{ij}(1 – \frac{E_{ij}}{N})$를 분산으로 하는 이항분포를 따릅니다. 그리고 표본크기가 충분히 크다면 $i$번째 행과 $j$번째 열의 범주(집단)의 관측빈도수의 표집분포는 정규분포에 근사하고 다음식으로 표현할 수 있습니다.
$$O_{ij} ∼ N(E_{ij}, E_{ij})$$
여기서, $O_{ij}$는 확률변수이며 $\text{집단}_{ij}$의 관측빈도수
이 정규분포를 표준정규분포로 변환하면 다음과 같습니다.
$$\dfrac{O_{ij} – E_{ij}}{\sqrt{E_{ij}}} =Z_{ij}∼ N(0, 1)$$
각 집단의 표준정규분포를 나타내는 $Z_{ij}$의 제곱을 모두 더한 것은 확률변수이고 카이제곱($\chi^2$)이라 합니다. 카이제곱은 카이제곱분포를 나타냅니다. 이 때 표본의 집단의 자유도는 (r-1)(c-1)이 됩니다.
$$\sum_{i=1}^{r}\sum_{j=1}^{c}\dfrac{(O_{ij} – E_{ij})^2}{E_{ij}}=\chi^2 ∼ \chi^2_{(r-1)(c-1)}$$
여기서, (r-1)(c-1)은표본의 집단의 자유도
표본의 자유도 등식
표본내 관측빈도 집단의 자유도 = 행 관측빈도 집단의 자유도 + 열 관측빈도 집단의 자유도 + 표본 상대빈도 집단의 자유도
$$(r \times c-1)=(r-1)+(c-1)+(r-1)(c-1)$$
여기서, $r$과 $c$는 행과 열의 두 범주형 확률변수값의 개수
가설검정
가설
귀무가설 $H_{0}$ : 범주형 확률변수 $A$로 구분되는 범주형 확률변수 $B$의 확률분포는 동일하다.
대립가설 $H_{1}$ : 범주형 확률변수 $A$로 구분되는 범주형 확률변수 $B$의 확률분포는 동일하지 않다.
검정통계량
$$\mathop{\sum}\limits_{{i}{=}{1}}\limits^{r}{\mathop{\sum}\limits_{{j}{=}{1}}\limits^{c}{\frac{{\left({{O}_{ij}{-}{E}_{ij}}\right)}^{2}}{{E}_{ij}}}}$$
여기서 $O_{ij}$는 관측빈도수
$E_{ij}$는 기대빈도수
그리고 $r$은 행으로 표현되는 범주형변수의 속성의 개수이고, $c$는 열로 표현되는 범주형변수의 속성의 개수입니다.
새로운 확률변수의 확률분포는 근사적으로 자유도가 $(r-1)(c-1)$인 $\chi^2$분포를 따릅니다.
$$\sum_{i=1}^{r}\sum_{j=1}^{c}\dfrac{(O_{ij} – E_{ij})^2}{E_{ij}}=\chi^2 ∼ \chi^2_{(r-1)(c-1)}$$
여기서, (r-1)(c-1)은표본의 집단의 자유도
귀무가설($H_{0}$) 기각역 – 유의수준이 $α$일 때
$$\chi_{obs}^{2}=\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{c}\dfrac{\left(O_{ij}-E_{ij}\right)^2}{E_{ij}}>\chi^2_{(r-1)(c-1);\alpha}$$
여기서 $\chi_{obs}^2$은 검정통계량
$O_{ij}$는 관측빈도수
$E_{ij}$는 기대빈도수
$\alpha$는 유의수준
두 범주형 확률변수의 관찰도수분포표 : 관찰도수($O_{ij}$)의 $r\times c$ 교차표
| 관찰도수 $O_{ij}$ | 범주형 확률변수 $A$ | 행의 합 | ||||
| $A_{1}$ | $A_{2}$ | $\cdots$ | $A_{c}$ | |||
| 범주형 확률변수 $B$ |
$B_{1}$ |
$O_{11}$ |
$O_{12}$ |
$\cdots$ |
$O_{1c}$ |
$T_{1\cdot}$ |
|
$B_{2}$ |
$O_{21}$ |
$O_{22}$ |
$\cdots$ |
$O_{2c}$ |
$T_{2\cdot}$ |
|
|
$\cdots$ |
$\cdots$ |
$\cdots$ |
$\cdots$ |
$\cdots$ |
$\cdots$ |
|
|
$B_{r}$ |
$O_{r1}$ |
$O_{r2}$ |
$\cdots$ |
$O_{rc}$ |
$T_{r\cdot}$ |
|
| 열의 합 | $T_{\cdot 1}$ | $T_{\cdot 2}$ | $\cdots$ | $T_{\cdot c}$ | $n$ | |
두 범주형 확률변수의 기대도수분포표 : 기대도수($E_{ij}$)의 $r\times c$ 교차표
| 기대도수 $E_{ij}$ | 범주형 확률변수 $A$ | 행의합 | ||||
| $A_{1}$ | $A_{2}$ | $\cdots$ | $A_{c}$ | |||
| 범주형 확률변수 $B$ | $B_{1}$ | $E_{11}=T_{1\cdot}\dfrac{T_{\cdot 1}}{n}$ | $E_{12}=T_{1\cdot}\dfrac{T_{\cdot 2}}{n}$ | $\cdots$ | $E_{1c}=T_{1\cdot}\dfrac{T_{\cdot c}}{n}$ | $T_{1\cdot}$ |
| $B_{2}$ | $E_{21}=T_{2\cdot}\dfrac{T_{\cdot 1}}{n}$ | $E_{22}=T_{2\cdot}\dfrac{T_{\cdot 2}}{n}$ | $\cdots$ | $E_{2c}=T_{2\cdot}\dfrac{T_{\cdot c}}{n}$ | $T_{2\cdot}$ | |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | |
| $B_{r}$ | $E_{r1}=T_{r\cdot}\dfrac{T_{\cdot 1}}{n}$ | $E_{r2}=T_{r\cdot}\dfrac{T_{\cdot 2}}{n}$ | $\cdots$ | $E_{rc}=T_{r\cdot}\dfrac{T_{\cdot c}}{n}$ | $T_{r\cdot}$ | |
| 열의 합 | $T_{\cdot 1}$ | $T_{\cdot 2}$ | $\cdots$ | $T_{\cdot c}$ | $n$ | |
두 범주형 확률변수의 카이제곱 확률분포표 : 카이제곱($\chi^2$)의 $r \times c$ 교차표
| $Z^2$ | 범주형 변수 $B$ | 행의 합 | ||||
| $B_{1}$ | $B_{2}$ | $\cdots$ | $B_{c}$ | |||
범주형 변수 $A$ | $A_{1}$ | $\dfrac{(O_{11}-E_{11})^2}{E_{11}}$ | $\dfrac{(O_{12}-E_{12})^2}{E_{12}}$ | $\cdots$ | $\dfrac{(O_{1c}-E_{1c})^2}{E_{1c}}$ | $$\sum_{j=1}^{c}\dfrac{(O_{1j}-E_{1j})^2}{E_{1j}}$$ |
| $A_{2}$ | $\dfrac{(O_{21}-E_{21})^2}{E_{21}}$ | $\dfrac{(O_{22}-E_{22})^2}{E_{22}}$ | $\cdots$ | $\dfrac{(O_{2c}-E_{2c})^2}{E_{2c}}$ | $$\sum_{j=1}^{c}\dfrac{(O_{2j}-E_{2j})^2}{E_{2j}}$$ | |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | |
| $A_{r}$ | $\dfrac{(O_{r1}-E_{r1})^2}{E_{r1}}$ | $\dfrac{(O_{r2}-E_{r2})^2}{E_{r2}}$ | $\cdots$ | $\dfrac{(O_{rc}-E_{rc})^2}{E_{rc}}$ | $$\sum_{j=1}^{c}\dfrac{(O_{rj}-E_{rj})^2}{E_{rj}}$$ | |
| 열의 합 | $$\sum_{i=1}^{r}\dfrac{(O_{i1}-E_{i1})^2}{E_{i1}}$$ | $$\sum_{i=1}^{r}\dfrac{(O_{i2}-E_{i2})^2}{E_{i2}}$$ | $\cdots$ | $$\sum_{i=1}^{r}\dfrac{(O_{ic}-E_{ic})^2}{E_{ic}}$$ | $$\sum_{i=1}^{r}\sum_{j=1}^{c}\dfrac{(O_{ij}-E_{ij})^2}{E_{ij}}$$ $$ \sim \chi_{(r-1)(c-1)}^2$$ | |
교차분석 카이제곱검정표
| 귀무가설($H_0$) | 검정통계량 | 대립가설($H_1$) | 귀무가설 기각역 |
| $\chi_{obs}^2=0$ | $\chi_{obs}^2=\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{c}\dfrac{(O_{ij}-E_{ij})^2}{E_{ij}}$ | $\chi_{obs}^2<0$ | $\chi_{obs}^2<-\chi^2_{(r-1)(c-1)\ ;\ \alpha}$ |
| $\chi_{obs}^2>0$ | $\chi_{obs}^2>\chi^2_{(r-1)(c-1)\ ;\ \alpha}$ | ||
| $\chi_{obs}^2\neq0$ | $\left|\chi_{obs}^2\right|>\chi^2_{(r-1)(c-1)\ ;\ \frac{\alpha}{2}}$ |