Home » DATA TRAINING » 코딩-1_2_3
데이터
프레임, 시각화, 설명
모델링
연구계획, 확률모델, 통계모델, 실험설계
데이터분석
모수비교
프레임
표본종류, 확률변수 가정
확률모델
새로운 확률변수, 표집
통계모델
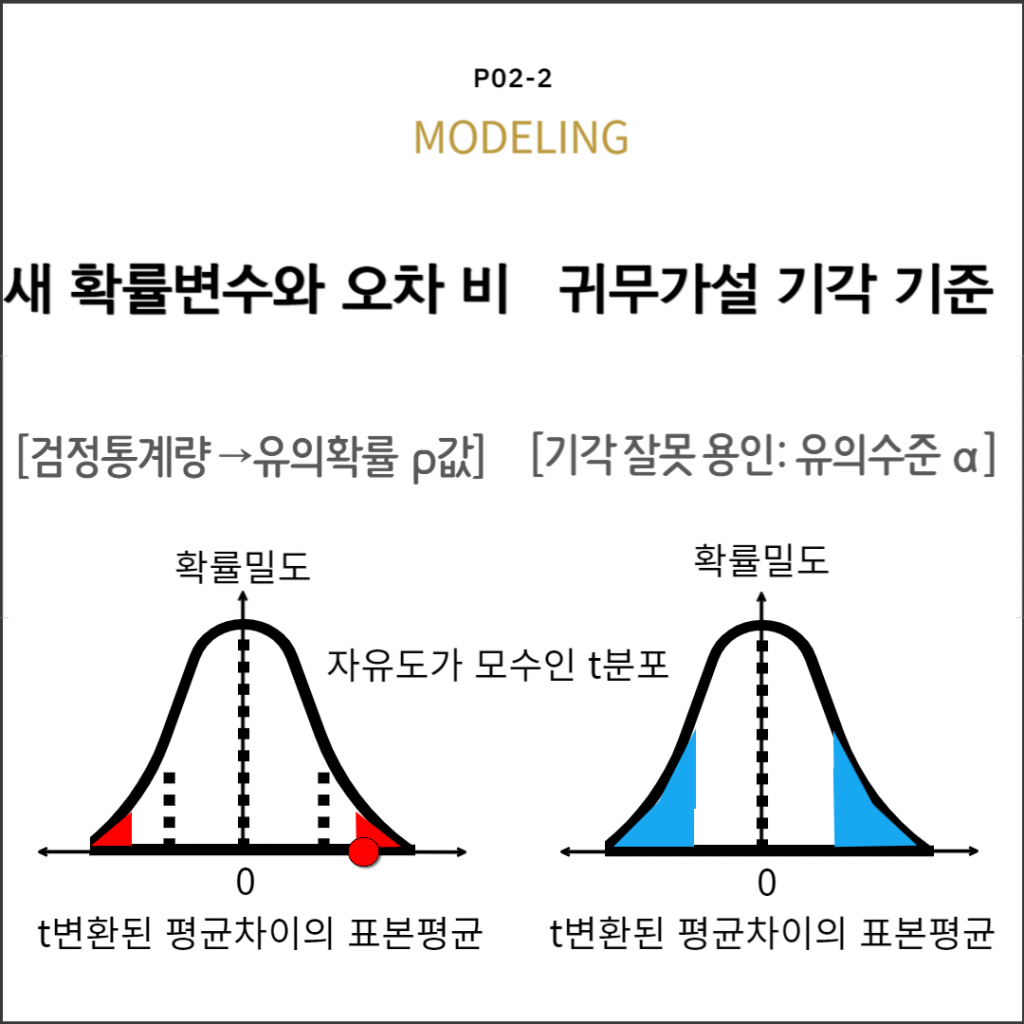
검정확률분포, 검정통계량
모수비교
귀무가설, 검정
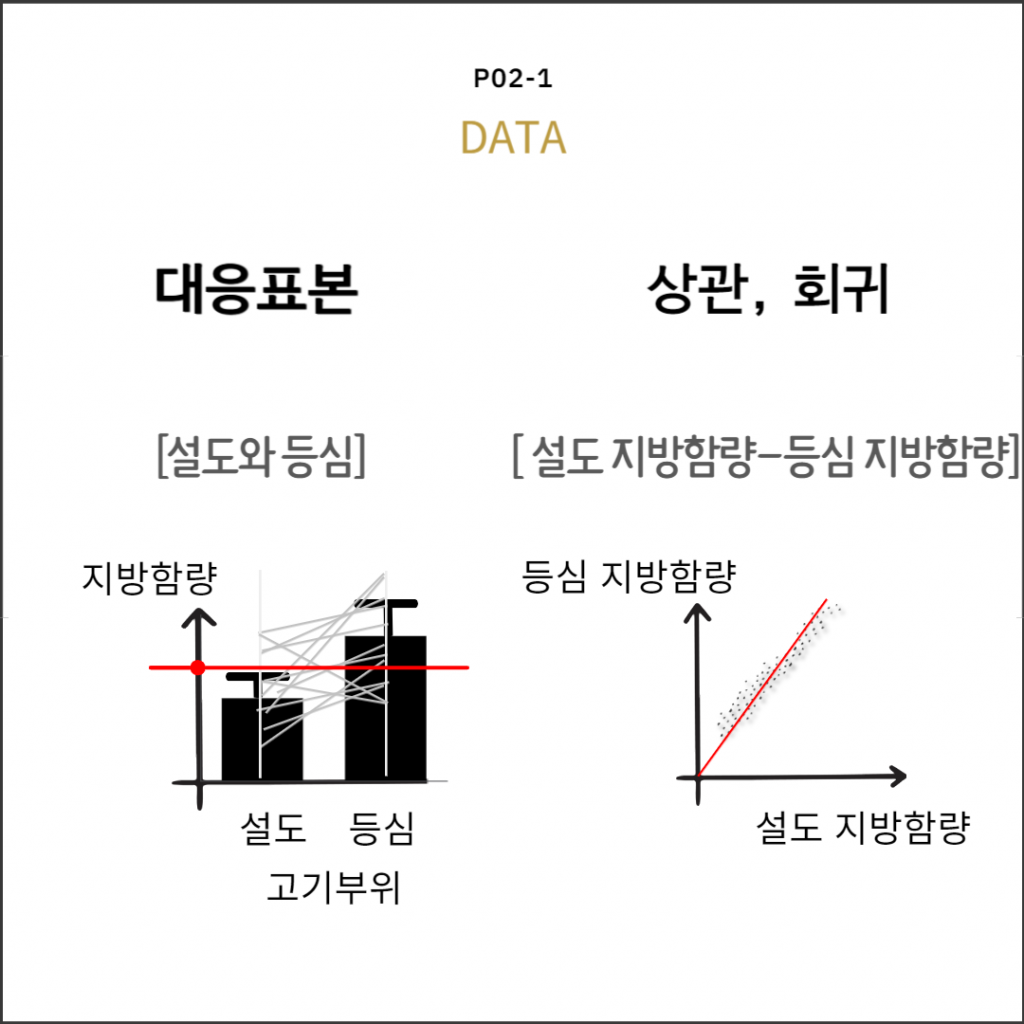
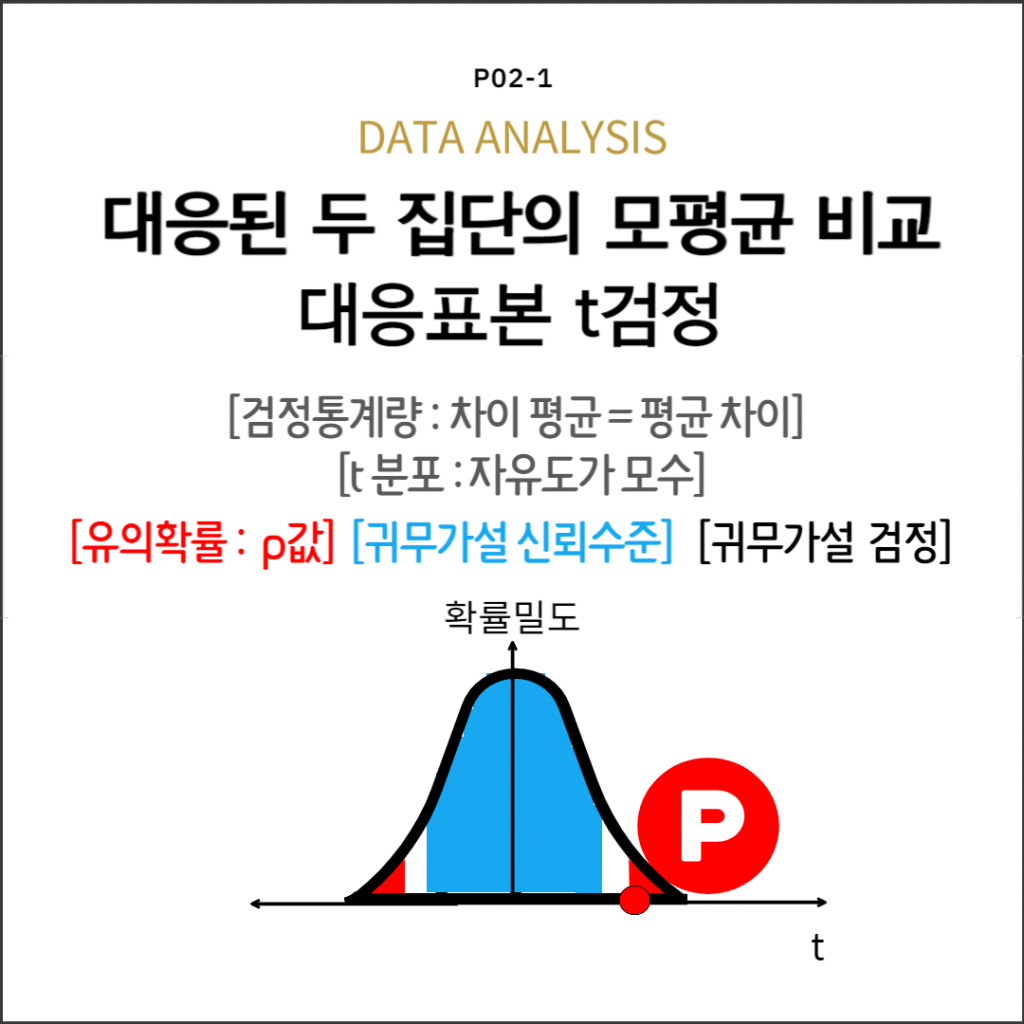
대응표본: 두 집단
등분산성, 독립성, 정규성
값차이
표본평균 중심극한정리
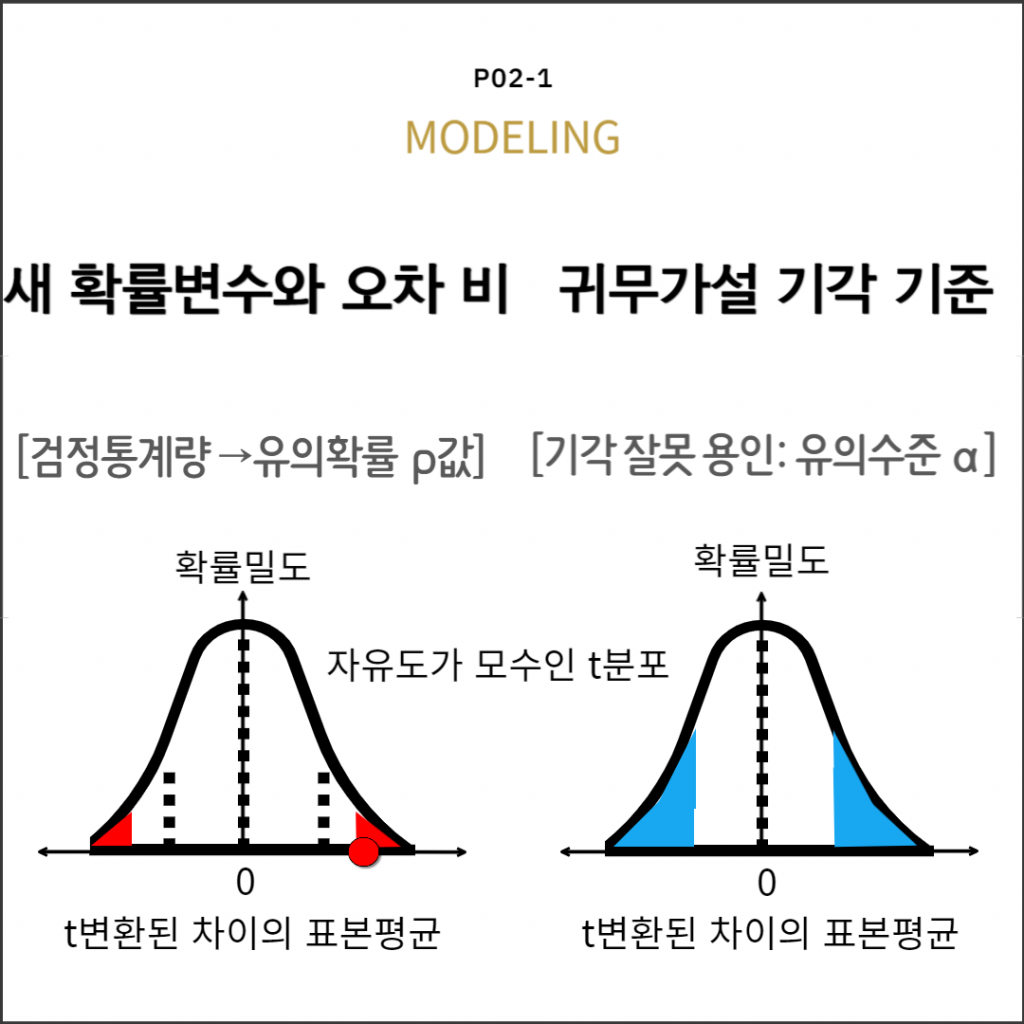
t분포
차이평균과 오차의 비
지방함량 차이평균은 0
유의확률과 유의수준으로 판정
정규분포
$$f(y \, ; \mu_Y, \sigma_Y^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right)$$
여기서, $y$는 정규분포를 나타내는 확률변수, $Y$의 값(변량)
$\mu_Y$는 확률변수, $Y$의 기대값: 집단의 모평균
$\sigma_Y^2$는 확률변수, $Y$의 모분산: 집단의 모분산
확률변수 t
$$t = \dfrac{Z}{\sqrt{\dfrac{V} {\nu}}}$$
여기서, $Z$는 표준정규분포를 나타내는 확률변수
$V$는 자유도 $\nu$의 $\chi^2$분포를 나타내는 확률변수
$\nu$는 $V$의 자유도
t분포
$$f(t \, ; \nu)=\dfrac{\Gamma \left({\frac{\nu +1}{2}}\right)}{\sqrt{\nu \pi}\Gamma \left(\dfrac{\nu }{2}\right)}\left(1+\dfrac {t^2}{\nu }\right)^{-\frac{\nu +1}{2}}$$
여기서, $f(\,\,)$는 확률밀도함수
$t$는 t분포를 나타내는 확률변수의 값(변량)
$\nu$는 자유도로 모수(매개변수, parameter)
$\Gamma(\,\,)$는 감마함수
대응표본 차이의 확률분포 (확률변수의 정규성가정에 의해 $f$는 정규분포)
$$f(d_i \, ; 0, \sigma_D^2)=\dfrac{1}{\sqrt{2\pi}\sigma_D} \mathrm{exp} \left(-\dfrac{d^2_i}{2 \sigma_D^2}\right)$$
여기서, $d_i$는 두 집단의 $i$번째 대응된 확률변수값의 차이: $d_i=y_{i1}-y_{i2}$
$d_i$는 연속형 확률변수: $d_i=D$ if $(i=1) \rightarrow (i=\infty)$
$D$는 연속형 확률변수
$\sigma_D^2$은 확률변수 $D$의 모분산
대응표본 차이의 분산 (대응표본은 공분산이 존재)
$$\sigma^2_{D}=\sigma^2_{(Y_{1}-Y_{2})} = \sigma^2_{Y_{1}} + \sigma^2_{Y_{2}}- 2\sigma_{Y_{1} Y_{2}}$$
여기서, $D$는 확률변수이며 대응된 확률변수인 $Y_{1}$과 $Y_{2}$의 차이: $D=Y_1-Y_2$
$\sigma^2_{D}$는 확률변수 $D$의 모분산
$\sigma^2_{Y_{1}}$는 확률변수 $Y_1$의 모분산
$\sigma^2_{Y_{2}}$는 확률변수 $Y_2$의 모분산
$\sigma_{Y_{1} Y_{2}}$는 대응된 확률변수인 $Y_1$과 $Y_2$의 모공분산
$${\rm Var}[D]={\rm Var}[Y_1-Y_2]= {\rm Var}[Y_1] + {\rm Var}[Y_2] – 2{\rm Cov}[Y_1, Y_2]$$
여기서, $D$는 대응된 확률변수인 $Y_1$과 $Y_2$의 차이이며 확률변수: $D=Y_1-Y_2$
${\rm Var}[D]$는 확률변수 $D$의 분산
${\rm Var}[Y_1]$는 확률변수 $Y_1$의 분산
${\rm Var}[Y_2]$는 확률변수 $Y_2$의 분산
${\rm Cov}[Y_1, Y_2]$는 대응된 확률변수인 $Y_1$과 $Y_2$의 공분산이며 확률변수
코시-슈바르츠 부등식
$$|\text{Cov}[Y_1, Y_2]| \leq \sqrt{\text{Var}[Y_1] \cdot \text{Var}[Y_2]}$$
$$(E[Y_1Y_2])^2 \leq E[Y_1^2] \cdot E[Y_2^2]$$
코시-슈바르츠 부등식을 확률변수차이에 적용
$$\text{Var}[Y_1] + \text{Var}[Y_2] – 2\sqrt{\text{Var}[Y_1] \cdot \text{Var}[Y_2]}$$
$$ \leq \text{Var}[D] $$
$$\leq \text{Var}[Y_1] + \text{Var}[Y_2] + 2\sqrt{\text{Var}[Y_1] \cdot \text{Var}[Y_2]}$$
여기서, $D$는 대응된 확률변수인 $Y_1$과 $Y_2$의 차이이며 확률변수: $D=Y_1-Y_2$
${\rm Var}[D]$는 확률변수 $D$의 모분산
${\rm Var}[Y_1]$는 확률변수 $Y_1$의 모분산
${\rm Var}[Y_2]$는 확률변수 $Y_2$의 모분산
${\rm Cov}[Y_1, Y_2]$는 대응된 확률변수 $Y_1$과 $Y_2$의 공분산이며 확률변수
대응표본 차이평균(mean difference) 표집의 확률분포 (확률변수의 정규성가정에 의해 $f$는 정규분포)
$$f(\bar {d} \, ; 0, \sigma^2_{\bar D})=\dfrac{1}{\sqrt{2\pi}\sigma_{\bar D}}\mathrm{exp} \left(-\dfrac{{\bar d}^2}{2\sigma^2_{\bar D}}\right)$$
여기서, $\bar {d}$는 차이의 평균값
$\sigma_{\bar D}^2$은 확률변수 $\bar D$의 모분산
대응표본 Z검정의 검정통계량 (귀무가설)
$$z = \dfrac{\bar{d}-d_0}{\dfrac{\sigma_D}{\sqrt{n}}}$$
여기서, $\bar d$는 차이평균의 관측값: $\bar d=\bar y_{\cdot 1}-y_{\cdot 2}$
$d_0$는 귀무가설로 주어지는 모평균차이: $\mu_{Y_1}-\mu_{Y_2}=d_0$
$\sigma_D$는 확률변수 $D$의 모표준편차
$n$은 대응표본크기(대응쌍의 수)
대응표본 t검정의 검정통계량 (귀무가설): Z검정의 $\sigma_{D}$를 $s_D$로 대체
$$t = \dfrac{\bar{d}-d_0}{\dfrac{s_D}{\sqrt{n}}}$$
여기서, $\bar d$는 차이평균의 관측값: $\bar d=\bar y_{\cdot 1}-y_{\cdot 2}$
$d_0$는 귀무가설로 주어지는 모평균차이: $\mu_{Y_1}-\mu_{Y_2}=d_0$
$s_D$는 확률변수 $D$의 표본표준편차
$n$은 대응표본크기(대응쌍의 수)
대응표본 t검정표
| 귀무가설($H_0$) | 검정통계량 | 대립가설($H_1$) | 귀무가설 기각역 |
| $$\mu_{Y_1}-\mu_{Y_2}=d_0$$ | $$t=\dfrac{\bar{d}-d_0}{\dfrac{s_D}{\sqrt{n}}}$$ | $$\mu_{Y_1}-\mu_{Y_2}\gt d_0$$ | $$\dfrac{\bar{d}-d_0}{\dfrac{s_D}{\sqrt{n}}}\gt t_{n-1\ ;\ \alpha}$$ |
| $$\\mu_{Y_1}-\mu_{Y_2}\lt d_0$$ | $$\dfrac{\bar{d}-d_0}{\dfrac{s_D}{\sqrt{n}}}\lt-t_{n-1\ ;\ \alpha}$$ | ||
| $$\\mu_{Y_1}-\mu_{Y_2}\ne d_0$$ | $$\left|\dfrac{\bar{d}-d_0}{\dfrac{s_D}{\sqrt{n}}}\right|\gt t_{n-1\ ;\ \frac{\alpha}{2}}$$ |
정규분포
$$f(y \, ; \mu_Y, \sigma_Y^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right)$$
여기서, $y$는 정규분포를 나타내는 확률변수, $Y$의 값(변량)
$\mu_Y$는 확률변수, $Y$의 기대값: 집단의 모평균
$\sigma_Y^2$는 확률변수, $Y$의 모분산: 집단의 모분산
확률변수 t
$$t = \dfrac{Z}{\sqrt{\dfrac{V} {\nu}}}$$
여기서, $Z$는 표준정규분포를 나타내는 확률변수
$V$는 자유도 $\nu$의 $\chi^2$분포를 나타내는 확률변수
$\nu$는 $V$의 자유도
t분포
$$f(t \, ; \nu)=\dfrac{\Gamma \left({\frac{\nu +1}{2}}\right)}{\sqrt{\nu \pi}\Gamma \left(\dfrac{\nu }{2}\right)}\left(1+\dfrac {t^2}{\nu }\right)^{-\frac{\nu +1}{2}}$$
여기서, $t$는 t분포를 나타내는 확률변수의 값(변량)
$\nu$는 자유도
$\Gamma(\,\,)$는 감마함수
독립표본 차이의 확률분포 (확률변수의 정규성가정에 의해 $f$는 정규분포)
$$f(d \, ; 0, \sigma_D^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{d^2}{2\sigma_D^2}\right)$$
여기서, $d$는 독립된 두 확률변수값인 $y_1$과 $y_2$ 의 차이이며 연속형 확률변수인 $D$의 확률변수값: $d=y_1-y_2$
$D$는 독립된 두 확률변수인 $Y_1$과 $Y_2$의 차이이며 확률변수: $D=Y_1-Y_2$
$\sigma_D^2$은 확률변수, $D$의 모분산: $\sigma_D^2=\sigma_{Y_1}^2+\sigma_{Y_2}^2$
독립표본 차이의 분산 (독립표본의 공분산은 0)
$$\sigma^2_{D}=\sigma^2_{(Y_{1}-Y_{2})} = \sigma^2_{Y_{1}} + \sigma^2_{Y_{2}}$$
여기서, $D$는 독립된 두 확률변수인 $Y_{1}$과 $Y_{2}$의 차이이며 확률변수
$\sigma^2_{D}$는 확률변수 $D$의 분산
$\sigma^2_{Y_{1}}$는 확률변수 $Y_1$의 분산
$\sigma^2_{Y_{2}}$는 확률변수 $Y_2$의 분산
$${\rm Var}[D] = {\rm Var}[Y_1] + {\rm Var}[Y_2]$$
여기서, $D$는 독립된 두 확률변수인 $Y_1$과 $Y_2$의 차이이며 확률변수
${\rm Var}[D]$는 확률변수 $D$의 분산
${\rm Var}[Y_1]$는 확률변수 $Y_1$의 분산
${\rm Var}[Y_2]$는 확률변수 $Y_2$의 분산
독립표본 평균차이(difference of means)의 확률분포
$$\sigma^2_{\bar D}=\sigma^2_{(\bar{Y_{1}}-\bar{Y_{2}})} = \sigma^2_{\bar{Y_{1}}} + \sigma^2_{\bar{Y_{2}}}$$
$$\therefore \dfrac{\sigma_{D}^2}{n}=\dfrac{\sigma_{Y_1}^2}{n_1}+\dfrac{\sigma_{Y_2}^2}{n_2}$$
여기서, $\bar D$는 독립된 확률변수인 $Y_{1}$과 $Y_{2}$의 평균차이(difference of means)이며 확률변수: $\bar D=\bar{Y_{1}}-\bar{Y_{2}}$; $\bar d=\bar{d_{1}}-\bar{d_{2}}$
$\sigma^2_{\bar D}$는 확률변수 $\bar D$의 분산
$\sigma^2_{\bar{Y_{1}}}$는 확률변수 $\bar{Y_1}$의 분산
$\sigma^2_{\bar{Y_{2}}}$는 확률변수 $\bar{Y_2}$의 분산
$D$는 독립된 두 확률변수인 $Y_{1}$과 $Y_{2}$의 차이이며 확률변수
$\sigma^2_{D}$는 확률변수 $D$의 분산
$\sigma^2_{Y_{1}}$는 확률변수 $Y_1$의 분산
$\sigma^2_{Y_{2}}$는 확률변수 $Y_2$의 분산
$n$은 전체표본크기: $n=n_1+n_2$
$n_1$, $n_2$는 전체표본내 독립된 두 집단의 표본크기: $n_1+n_2=n$
독립표본 평균차이(difference of means) 표집의 확률분포 (확률변수의 정규성가정에 의해 $f$는 정규분포)
$$f(\bar {d} \, ; 0, \sigma^2_{\bar D})=\dfrac{1}{\sqrt{2\pi}\sigma_{\bar D}}\mathrm{exp} \left(-\dfrac{{\bar d}^2}{2\sigma^2_{\bar D}}\right)$$
여기서, $\bar {d}$는 평균차이값: $\bar d=\bar y_{1}-\bar y_{2}$
$\sigma_{\bar D}^2$은 확률변수 $\bar D$의 모분산
독립표본 Z검정의 검정통계량 (등분산가정, 귀무가설)
$$z =\dfrac{(\bar{y}_1 – \bar{y}_2)-d_0}{\dfrac{\sigma_{D}}{\sqrt{n}}}=\dfrac{(\bar{y}_1 – \bar{y}_2)-d_0}{\sqrt{\dfrac{\sigma^2_{Y_1}}{n_1} + \dfrac{\sigma^2_{Y_2}}{n_2}}}=\dfrac{(\bar{y}_1 – \bar{y}_2)-d_0}{{\sigma_{Y}}\sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}}}$$
여기서, $\bar{y}_1$, $\bar{y}_2$는 독립된 두 집단의 표본평균의 관측값
$d_0$는 귀무가설로 주어지는 모평균차이: $d_0=\mu_{Y_2}-\mu_{Y_1}$
$n$은 전체표본크기: $n=n_1+n_2$
$n_1$, $n_2$는 전체표본내 독립된 두 집단의 표본크기: $n_1+n_2=n$
등분산가정 (집단내분산은 같다): $ \sigma_{Y_1}^2=\sigma_{Y_2}^2=\sigma_Y^2$
독립표본 t검정의 검정통계량 (등분산가정, 귀무가설): Z검정의 $\sigma_{Y}$를 $s_p$로 대체
$$t =\dfrac{(\bar{y}_1 – \bar{y}_2)-d_0}{s_p \sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}}}$$
여기서, $\bar{y}_1$, $\bar{y}_2$는 독립된 두 집단의 표본평균의 관측값
$d_0$는 귀무가설로 주어지는 모평균차이: $d_0=\mu_{Y_2}-\mu_{Y_1}$
$n_1$, $n_2$는 독립된 두 집단의 표본크기: $n_1+n_2=n$
$n$은 전체표본크기: $n=n_1+n_2$
집단내변동 등식: $((n_1-1)+(n_2-1))\dfrac{s_p^2}{\sigma_Y^2}=(n_1-1)\dfrac{s_{Y_1}^2}{\sigma_{Y_1}^2}+(n_2-1)\dfrac{s_{Y_2}^2}{\sigma_{Y_2}^2}$
등분산가정 (집단내분산은 같다): $\sigma_Y^2= \sigma_{Y_1}^2=\sigma_{Y_2}^2$
통합표본분산 (pooled variance): $s_p = \sqrt{\dfrac{(n_1-1)s_{Y_1}^2 + (n_2-1)s_{Y_2}^2}{n_1 + n_2 – 2}}$
$s_{Y_1}^2$, $s_{Y_2}^2$는 독립된 두 집단의 표본분산
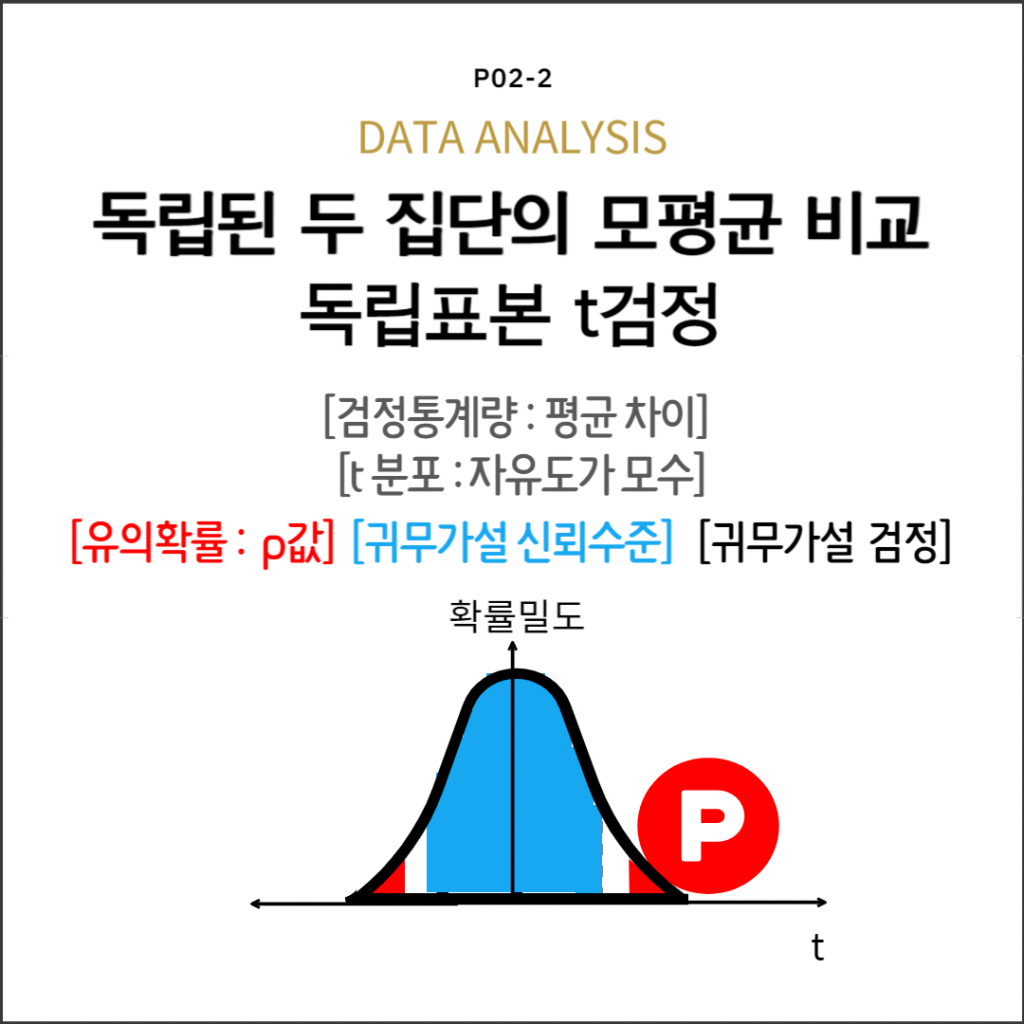
독립표본 t검정표: 두 모평균 비교
| 귀무가설($H_0$) | 검정통계량 | 대립가설($H_1$) | 귀무가설 기각역 |
| $\mu_{Y_1} – \mu_{Y_2}=d_0$ | $$t=\dfrac{(\bar{y}_1-\bar{y}_2)-d_0}{s_p\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}$$ 여기서, $s_p=\sqrt{\dfrac{(n_1-1)s_{1}^2+(n_2-1)s_{2}^2}{n_1+n_2-2}}$ | $\mu_{Y_1} – \mu_{Y_2} \gt d_0$ | $t \lt -t_{n-2\ ;\ \alpha}$ |
| $\mu_{Y_1} – \mu_{Y_2} \lt d_0$ | $t \gt t_{n-2\ ;\ \alpha}$ | ||
| $\mu_{Y_1} – \mu_{Y_2} \ne d_0$ | $\mid {t} \mid \gt t_{n-2\ ;\ \frac{\alpha}{2}}$ |
독립표본 F검정표: 집단(group)이 2개인 일원분산분석 F검정(집단간분산과 집단내분산 비교)
| 귀무가설($H_0$) | 검정통계량 | 대립가설($H_1$) | 귀무가설 기각역 |
독립된 두 집단의 모평균이 같다. $\mu_{1}=\mu_{2}=\mu_0$ $\beta_{0,1}=\beta_{0,2}=\beta_0$ $$\therefore \sigma_B^2=0$$ | $F=\dfrac{s_{B}^2}{s_{W}^2}=\dfrac{MS_{B}}{MS_{W}}$ $\sigma_B^2 \neq 0$인 경우 $\sigma_B^2 $과 $\sigma_W^2$의 크기 비교 $t=\sqrt{F}$ | $$\sigma_B^2\gt\sigma_W^2$$ | $$\dfrac{s_B^2}{s_W^2}\gt F_{n_B-1,\ n_W-1\ ;\ \alpha}$$ |
| $$\sigma_B^2\lt\sigma_W^2$$ | $$\dfrac{s_B^2}{s_W^2}\lt\ F_{n_B-1,\ n_W-1\ ;\ \alpha}$$ | ||
| $$\sigma_B^2\ne\sigma_W^2$$ | $$\dfrac{s_B^2}{s_W^2}\gt F_{n_B-1,\ n_W-1\ ;1-\frac{\alpha}{2}}$$ $$\dfrac{s_B^2}{s_W^2}\lt F_{n_B-1,\ n_W-1\ ;\ \frac{\alpha} {2}}$$ |
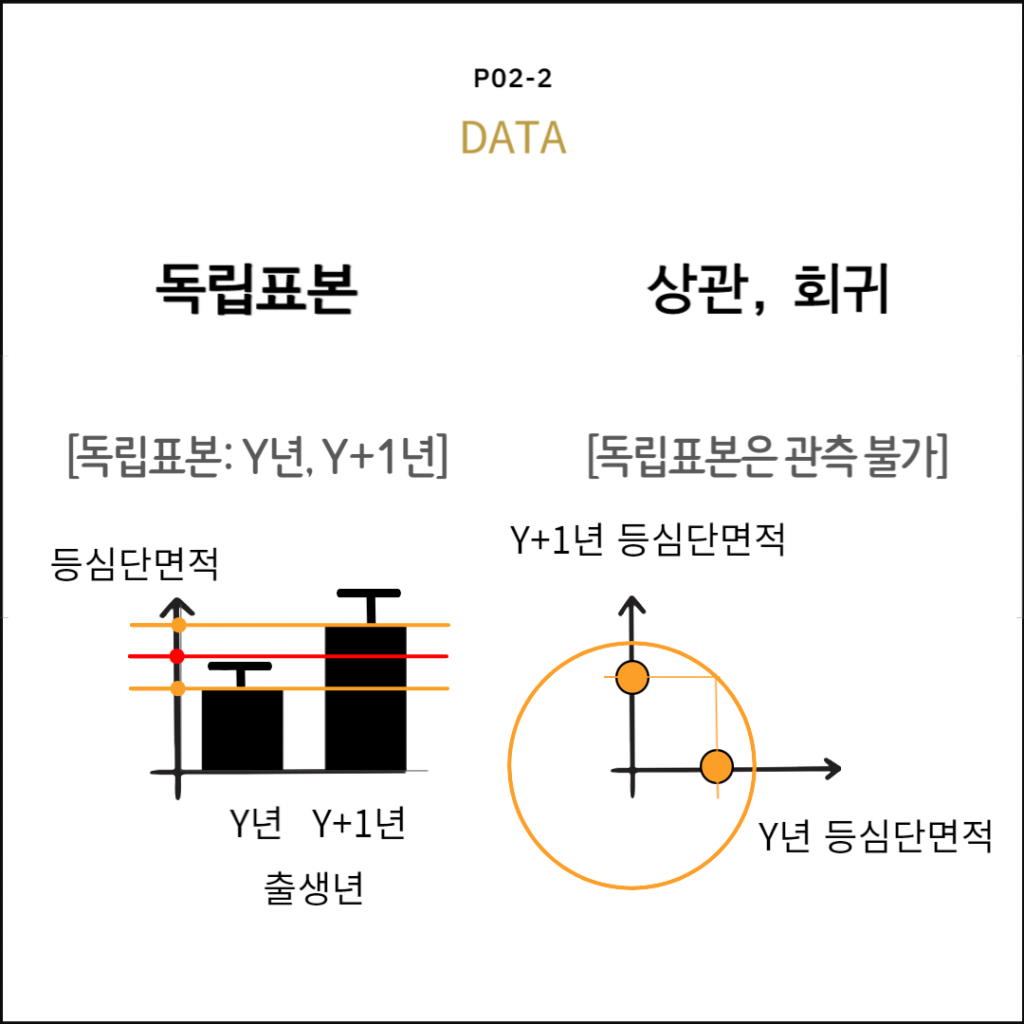
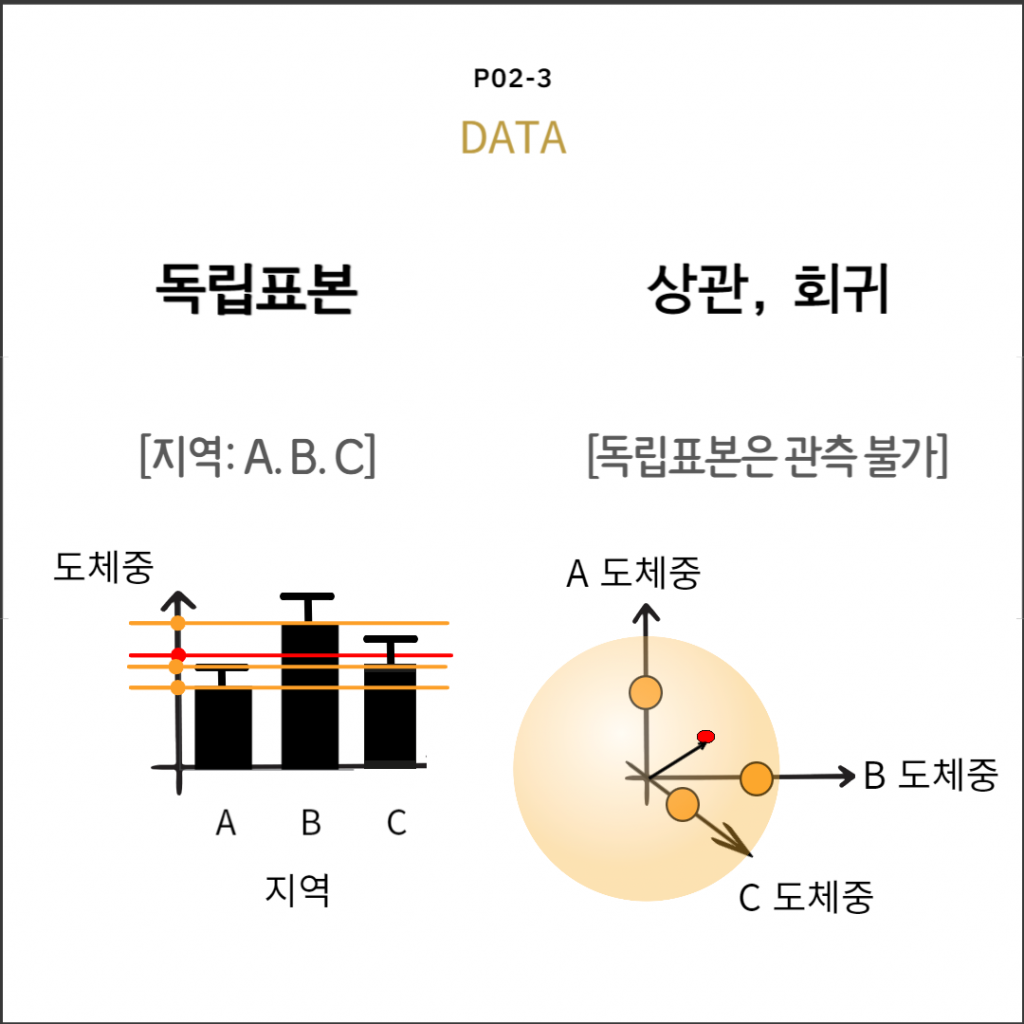
독립표본: 여러 집단
등분산성, 독립성, 정규성
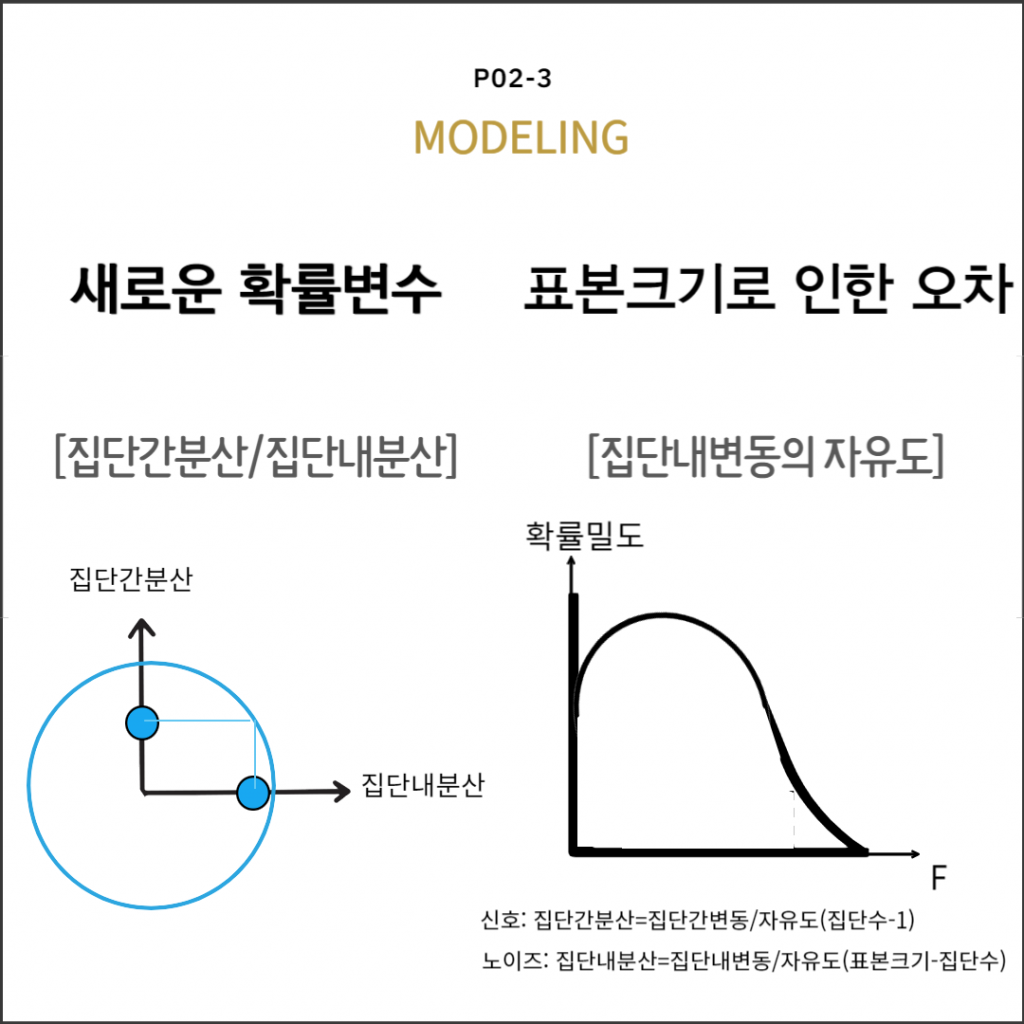
집단간분산/집단내분산
표본분산 중심극한정리
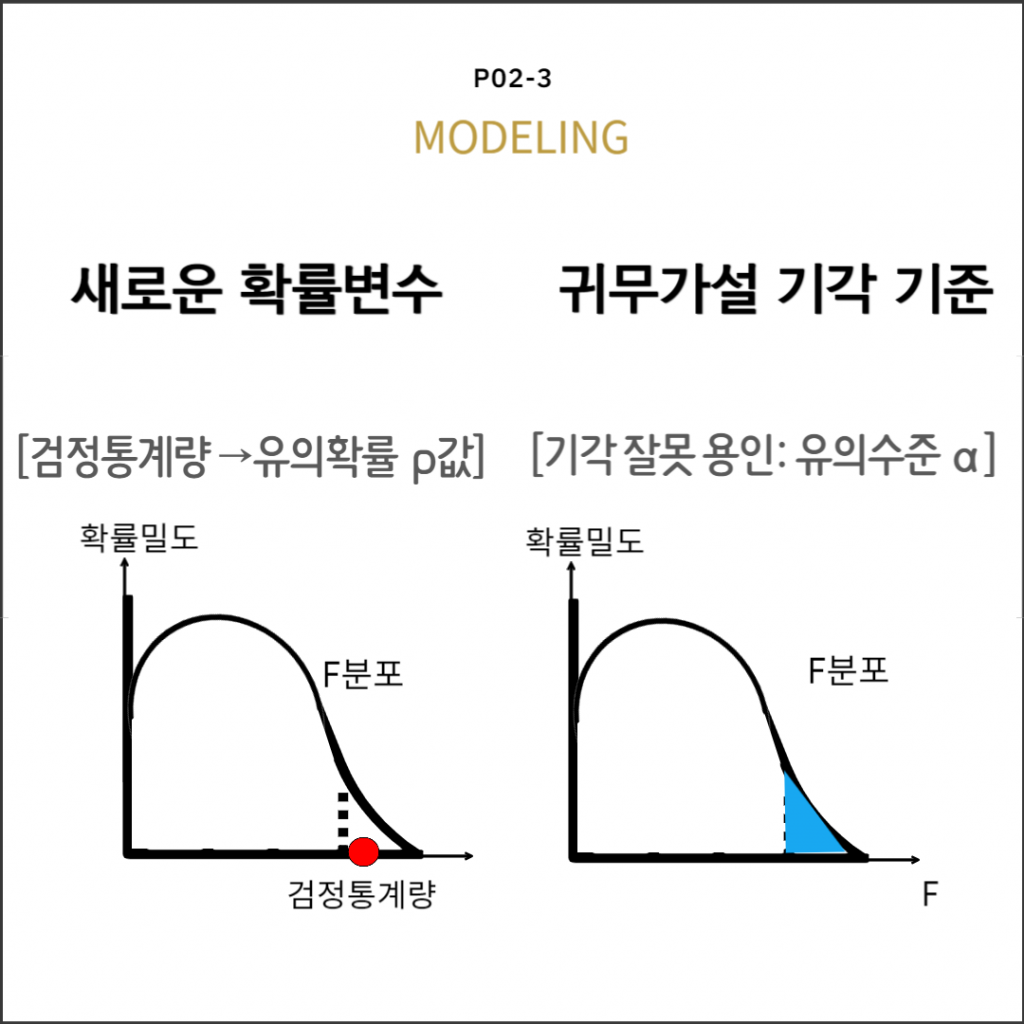
F분포
신호와 노이즈의 비
도체중의 지역에 따른 신호는 0
유의확률과 유의수준으로 판정
정규분포
$$f(y \, ; \mu_Y, \sigma_Y^2)=\dfrac{1}{\sqrt{2\pi}\sigma_Y} \mathrm{exp} \left(-\dfrac{(y-\mu_Y)^2}{2\sigma_Y^2}\right)$$
여기서, $y$는 정규분포를 나타내는 확률변수, $Y$의 값(변량)
$\mu_Y$는 확률변수, $Y$의 기대값: 집단의 모평균
$\sigma_Y^2$는 확률변수, $Y$의 모분산: 집단의 모분산
확률변수 카이제곱
$$\chi^2= Z_1^2 + Z_2^2 + \cdots = \sum\limits_{i=1}^{k}Z_{i}^2$$
여기서, $Z_i$는 표준정규분포 확률변수
$k$는 자유도: 표준정규분포 확률변수 개수
카이제곱분포
$$f(x \, ; k)=\dfrac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}$$
여기서, $x$는 카이제곱분포를 나타내는 확률변수의 값(변량)
$k$는 자유도: $Z^2$의 개수
확률변수 F
$$F = \dfrac{\frac{\chi^2_1}{df_1}}{\frac{\chi^2_2}{df_2}}$$
여기서, $F$는 F분포를 나타내는 확률변수
$\chi^2_1$과 $\chi^2_2$는 카이제곱분포를 나타내는 확률변수
$df_1$과 $df_2$는 $\chi^2_1$과 $\chi^2_2$가 나타내는 카이제곱분포의 자유도
F분포
$$f(x; df_1, df_2) = \frac{\left(\dfrac{df_1}{df_2}\right)^{\frac{df_1}{2}} x^{\frac{df_1}{2} – 1} \left(1 + \frac{df_1}{df_2}x\right)^{-\frac{df_1 + df_2}{2}}}{B\left(\frac{df_1}{2}, \frac{df_2}{2}\right)}
$$
여기서, $x$는 F분포를 나타내는 확률변수의 값(변량)
$df_1$과 $df_2$는 분자와 분모의 카이제곱분포의 자유도
$B(\,\,)$는 베타함수
$B(\frac{df_1}{2}, \frac{df_2}{2}) = \frac{\Gamma(\frac{df_1}{2}) \Gamma(\frac{df_2}{2})}{\Gamma(\frac{df_1}{2} + \frac{df_2}{2})}$
$\Gamma(\,\,)$는 감마함수
표본의 변동: Sample variation
$$SS_{Sample} =n \cdot{\bar y}^2+SS_{T}$$
여기서, $SS_{Sample}$는 0을 기준으로하는 표본의 변동
$\bar{y}$는 표본평균: bias
$n$은 표본크기
$SS_{T}$는 표본평균을 기준으로 하는 표본내 변동
변동분해공식: Variation decomposition formula
$$SS_{T} =SS_{B}+SS_{W}$$
여기서, $SS_{T}$는 표본평균 기준의 개체의 변동: 전체변동
$SS_{B}$는 표본평균 기준의 집단의 변동: 집단간변동
$SS_{W}$는 집단평균 기준의 개체의 변동: 집단내변동
자유도분해공식: Decomposition of $df$ formula
$$df_{T} =df_{B}+df_{W}$$
$$(n-1) =(k-1)+(n-k)$$
여기서, $df_{T}$는 표본의 자유도: $n-1$
$df_{B}$는 표본내 집단의 자유도: $k-1$
$df_{W}$는 표본내 개체의 자유도: $n-k$
$n$은 표본크기: 표본내 개체의 수
$k$는 집단의 수: 표본내 집단의 수
전체변동: Total variation
$$SS_T= \sum\limits_{j=1}^{k}\sum\limits_{i=1}^{n_j} (y_{ij} – \bar{y})^2$$
여기서, $SS_T$는 표본평균을 기준으로 하는 표본내 변동
$k$는 집단수
$n_j$는 $j$번째 집단의 표본크기
$y_{ij}$는 확률변수 $Y$의 $j$번째 집단의 $i$번째 값
$\bar y$는 표본평균
집단간변동: Between-group variation
$$SS_{B} = \sum\limits_{j=1}^{k} n_j (\bar{y}_j – \bar{y})^2$$
여기서, $SS_{B}$은 표본내 집단간변동
$k$는 집단수
$n_j$는 $j$번째 집단의 표본크기
$\bar {y}_{j}$는 $j$번째 집단의 표본평균
$\bar y$는 표본평균
집단내변동: Within-group variation
$$SS_W = \sum_{j=1}^{k} \sum_{i=1}^{n_j} (y_{ij} – \bar{y}_j)^2$$
여기서, $SS_W$는 표본내 집단내변동
$k$는 집단수
$n_j$는 $j$번째 집단의 표본크기: $\sum\limits_{j=1}^{k}n_{k}=n$; $n$은 표본크기
$y_{ij}$는 확률변수 $Y$의 $j$번째 집단의 $i$번째 값
$\bar {y}_{j}$는 $j$번째 집단의 표본평균
집단간분산: Between-group mean square
$$MS_{B} = \dfrac{SS_B}{k-1}$$
여기서, $MS_{B}$는 집단간분산
$SS_{B}$는 집단간변동
$k$는 표본내 집단수
$(k-1)$은 표본내 집단의 자유도: $d_{B}$
집단내분산: Within-group mean square
$$MS_W = \dfrac{SS_W}{n-k}$$
여기서, $MS_W$는 집단내분산
$SS_W$는 집단내변동
$n$은 표본크기: $n=\sum\limits_{j=1}^{k}n_j$
$k$는 표본내 집단수
$(n-k)$는 표본내 개체의 자유도: $d_{W}$
표본에서 집단간변동의 표준화: 카이제곱($\chi^2_{B}$)
$$\chi^2_{B}={df_{B}}\dfrac{s_{B}^2}{\sigma_{B}^2}=(k-1)\dfrac{s_{B}^2}{\sigma_{B}^2}$$
여기서, $s_{B}^2$는 표본집단간분산
$\sigma_{B}^2$은 모집단간분산
$df_{B}$는 표본내 집단의 자유도: $df_{B}=k-1$
$k$는 표본내 집단수
표본에서 집단내변동의 표준화: 카이제곱($\chi^2_{W}$)
$$\chi^2_{W}={df_{W}}\dfrac{s_{W}^2}{\sigma_{W}^2}=(n-k)\dfrac{s_{W}^2}{\sigma_{W}^2}$$
여기서, $s_{W}^2$는 표본집단내분산
$\sigma_{W}^2$은 모집단내분산
$df_{W}$는 표본내 개체의 자유도: $df_{W}=n-k$
$n$은 표본내 개체수
$k$는 표본내 집단수
표본에서 확률변수 F
$$F= \dfrac{\dfrac{\chi^2_{B}}{df_{B}}}{\dfrac{\chi^2_{W}}{df_{W}}}=\dfrac{\dfrac{s_B^2}{\sigma_B^2}}{\dfrac{s_W^2}{\sigma_W^2}}$$
등분산가정
독립동일분포(Independent and Identically Distributed): 실현되기 전 개체의 확률분포의 분산은 같다.
$\rightarrow$ 등분산가정(등분산성): 실현된 모든 집단의 집단내분산은 같다.
귀무가설: 표본내 모든 집단(group)의 모평균이 같다
모든 집단의 모평균이 같다.
$\rightarrow$ 개체의 변동으로 인한 모집단내분산(모노이즈)과 모집단간분산(모신호)이 등가
$\rightarrow \sigma_W^2=\sigma_B^2$
F 검정통계량
$$F= \dfrac{\dfrac{\chi^2_{B}}{df_{B}}}{\dfrac{\chi^2_{W}}{df_{W}}}=\dfrac{\dfrac{s_B^2}{\sigma_B^2}}{\dfrac{s_W^2}{\sigma_W^2}}=\dfrac{MS_{B}}{MS_{W}}$$
여기서, $\sigma_{W}^2=\sigma_{B}^2$: 귀무가설
$\sigma_{B}^2$는 모집단간분산
$\sigma_{W}^2$는 모집단내분산
$s_{B}^2$는 표본집단간분산: $s_{B}^2=MS_{B}=\dfrac{SS_{B}}{k-1}$
$k$는 표본내 집단수
$s_{W}^2$는 표본집단내분산: $s_{W}^2=MS_{W}=\dfrac{SS_W}{n-k}$
$n$은 표본크기
일원분산분석 F검정표(집단간분산과 집단내분산 비교) : 독립된 여러 집단의 모평균 비교-정규분포 가정-등분산 가정
| 귀무가설$(H_0)$ | 검정통계량 | 대립가설$(H_1)$ | 귀무가설 기각역 |
독립된 여러 집단의 모평균($\mu_i$)이 같다. $\mu_{1}=\mu_{2}=\cdots=\mu_{k}=\mu_0$ $\beta_{0,1}=\beta_{0,2}=\cdots=\beta_{0,k}=\beta_0$ 여기서, $\mu_i$는 $i$번째 집단의 모평균 $\beta_{0,i}$는 $i$번째 집단의 모평균 $k$는 표본내 집단의 수 | $F=\dfrac{s_{B}^2}{s_{W}^2}=\dfrac{MS_{B}}{MS_{W}}$ | 적어도 한 $\mu_{i}$는 $\mu_0$보다 크다. 적어도 한 $\beta_{0,i}$는 $\beta_0$보다 크다. | 검정통계량으로 한 $\mu_{i}$가 $\mu_0$보다 큰 지 알 수 없다. 검정통계량으로 한 $\beta_{0,i}$가 $\beta_0$보다 큰 지 알 수 없다. |
적어도 한 $\mu_{i}$는 $\mu_0$보다 작다. 적어도 한 $\beta_{0,i}$는 $\beta_0$보다 작다. | 검정통계량으로 $\mu_{i}$가 $\mu_0$보다 작은 지 알 수 없다. 검정통계량으로 한 $\beta_{0,i}$가 $\beta_0$보다 작은 지 알 수 없다. | ||
적어도 한 $\mu_{i}$는 $\mu_0$이 아니다. 적어도 한 $\beta_{0,i}$는 $\beta_0$이 아니다. | $F>F_{k-1,\ n-k\ ;\ \alpha}$ 여기서, $k$는 표본내 집단의 수 $n$은 표본내 개체의 수: 표본크기 $\alpha$는 유의수준 |